Получаем две расчетные точки:
|
ω, 1/с |
77.7 |
68,1 |
|
М, Н∙м |
0 |
323.21 |
Номинальный ток возбуждения генератора
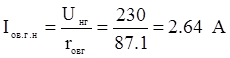 ; FВГН=IВГН*WВГ =2,64*1300=3432 А
; FВГН=IВГН*WВГ =2,64*1300=3432 А
![]() = 87,1 Ом
= 87,1 Ом
По кривой намагничивания генератора определяем номинальный поток:
ФГН=0,86∙106 МКС=0.0086 Вб
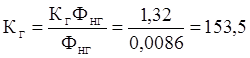
![]() 2∙31=62 1/c; М»МС=325,976
Н∙М
2∙31=62 1/c; М»МС=325,976
Н∙М
Определяем требуемый поток возбуждения генератора :
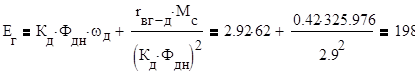 |
ω0= ЕГmax/КДФд=198/2,92=68 1/с
ЕГmax=КГФГmaxwГ Þ 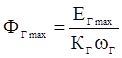 =198/153,5*151,8=0,0085 Вб;
=198/153,5*151,8=0,0085 Вб;
По кривой намагничивания генератора
FВГmax=3920А ; IВГmax=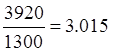 А;
А;
UВГmax=IВГmax∙rВГ=3.015∙87.1=262.7 В
![]() 0,57∙31=17,7 1/с; М»МС=325,976
нМ
0,57∙31=17,7 1/с; М»МС=325,976
нМ
 |
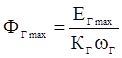 =67,8/153,5*151,8=0,0029 Вб
=67,8/153,5*151,8=0,0029 Вб
По кривой намагничивания генератора
FГMIN=1320 А ; IВГMIN=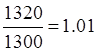 А; UВГMIN=IВГMIN*rВГ= 1,01∙87,1=88,3 В
А; UВГMIN=IВГMIN*rВГ= 1,01∙87,1=88,3 В
w=0 ; М=0; w0МЕХ=68,1 1/с ; М=-2,5МН =-325,976∙2.5=-816 Н∙м
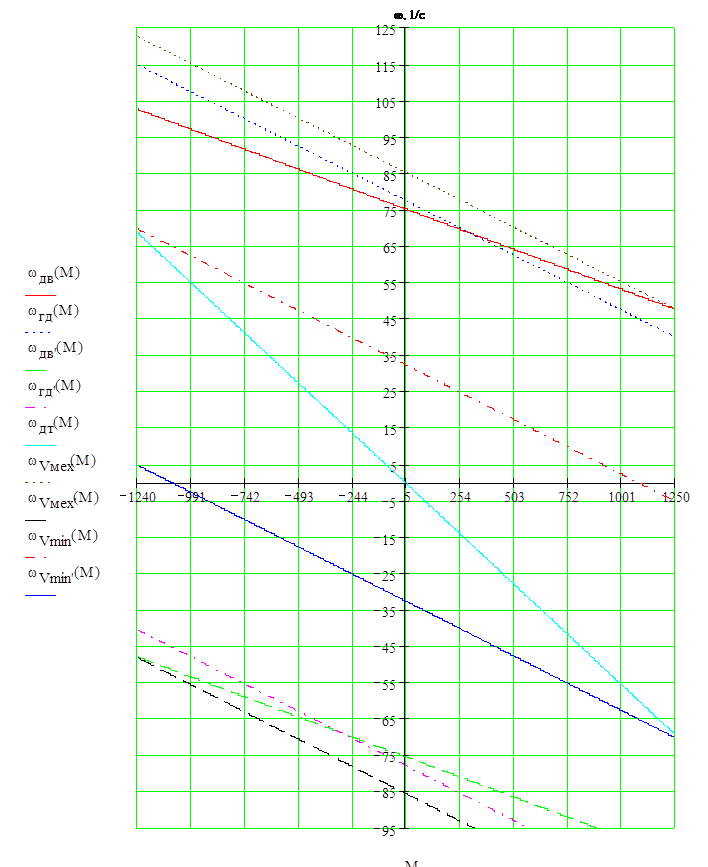
Все рассчитанные характеристики построены на рисунке 5.
 |
|
||||||||||||
|
||||||||||||
|
||||||||||||
|
||||||||||||
 |
||||||||||||
|
||||||||||||
4.7 Динамический расчет электропривода.
4.7.1 Математическое описание нелинейной системы Г-Д с принимаемыми допущениями.
Исходная система уравнений :
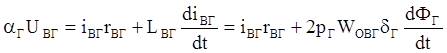 (1)
(1)
где 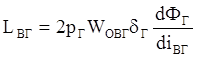
кривая намагничивания генератора
ФГ = f(FВГ) (2)
wГ=wАД=wС×(1-S) (3) ,
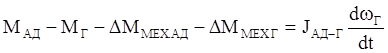 (4)
(4)
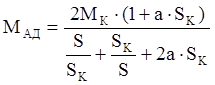 (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
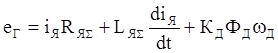 (8)
(8)
где 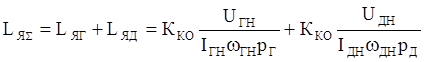 (9)
(9)
![]() (10)
(10)
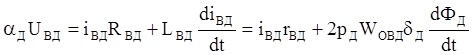 (11)
(11)
где 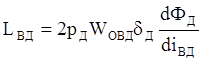
кривая намагничивания двигателя
ФД = f(iВД) (12)
![]() (13)
(13)
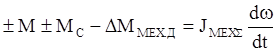 (14)
(14)
дифференциальные уравнения представим в форме Коши:
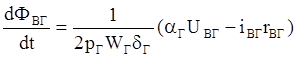 (1)’
(1)’
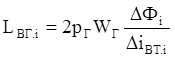
![]() (3)
(3)
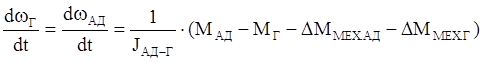 (4а)’
(4а)’
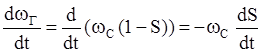 (4б)’
(4б)’
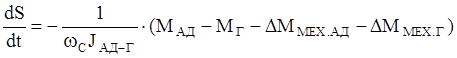 (4в)’
(4в)’
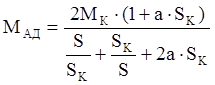 (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
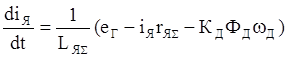 (8)’
(8)’
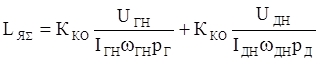 (9)
(9)
![]() (10)
(10)
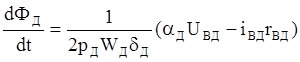 (11)’
(11)’
![]()
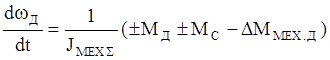 (14)’
(14)’
4.7.2 Составление структуры модели для математической модели динамических режимов.
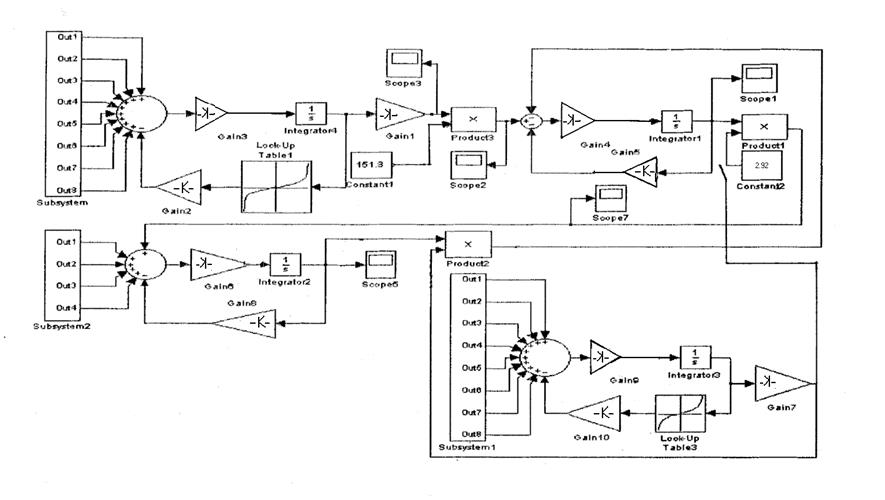
Модель данной
системы Г-Д в программе “MATLAB” представлены на рис.6,7,8.
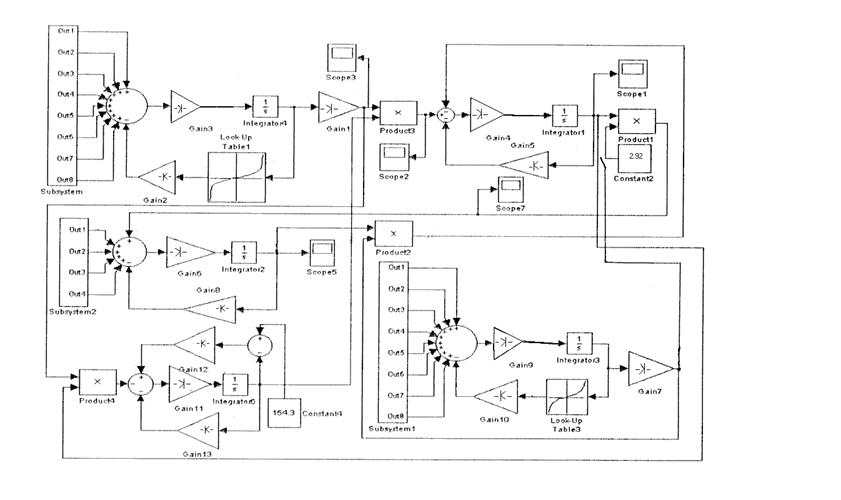
Рис.6
Рис.7
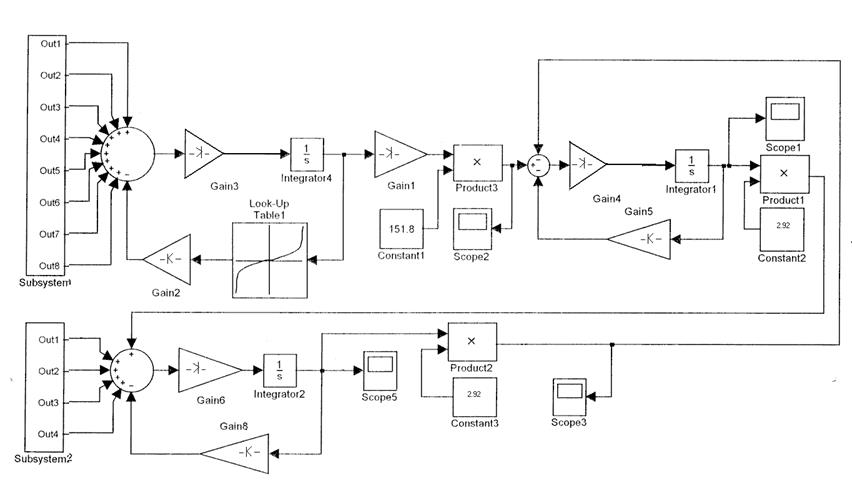
Рис.8
Смоделировав переходные процессы в программе “MATLAB” получаем следующие графики представленные ниже на рисунках.
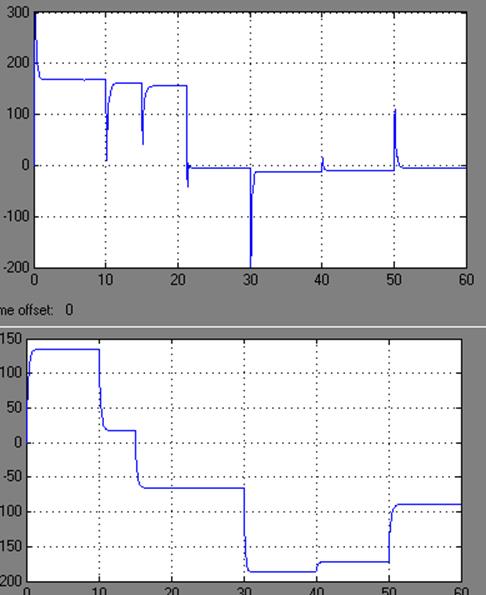 |
Переходные процессы при разгоне до ωmax
|
|
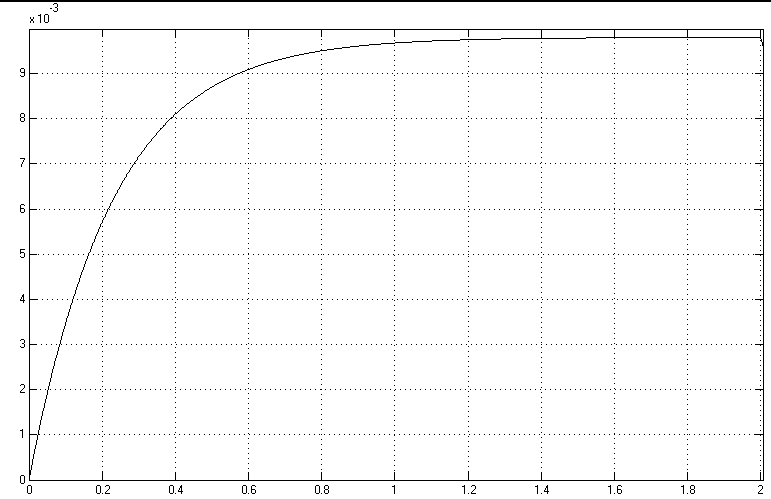
Рис.10 (поток генератора)
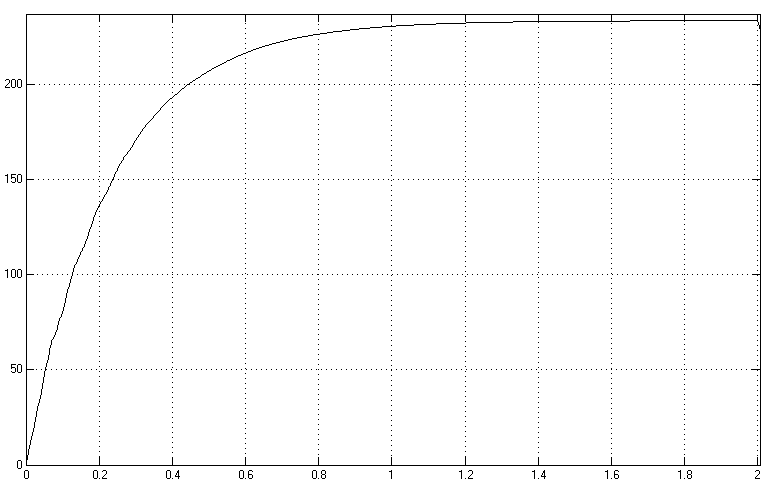 |
|
|
|
|
|
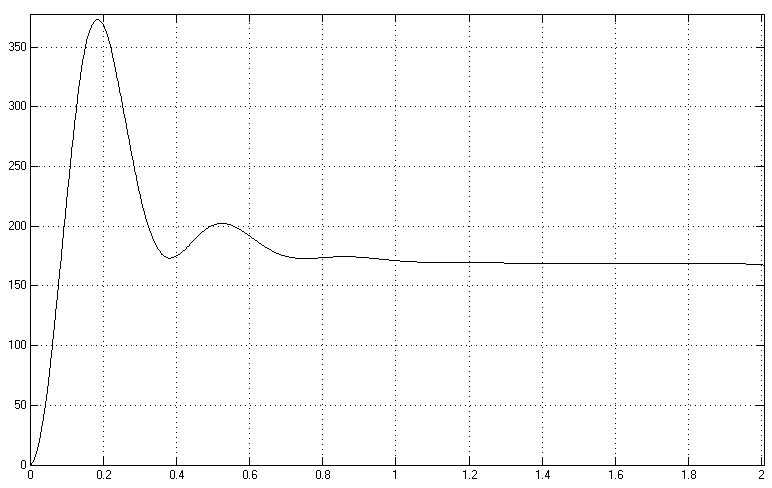
Рис.12 (ток двигателя)
Переходные процессы при торможении до ωmin
|
|
|
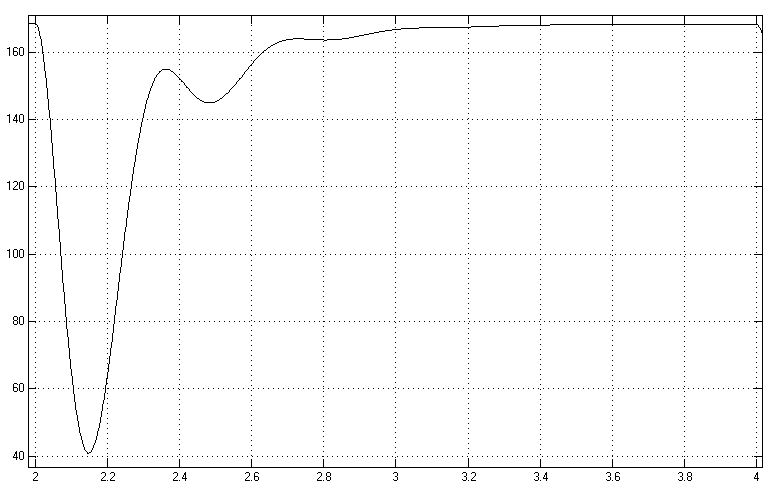
Рис.13 (ток двигателя)
|
|
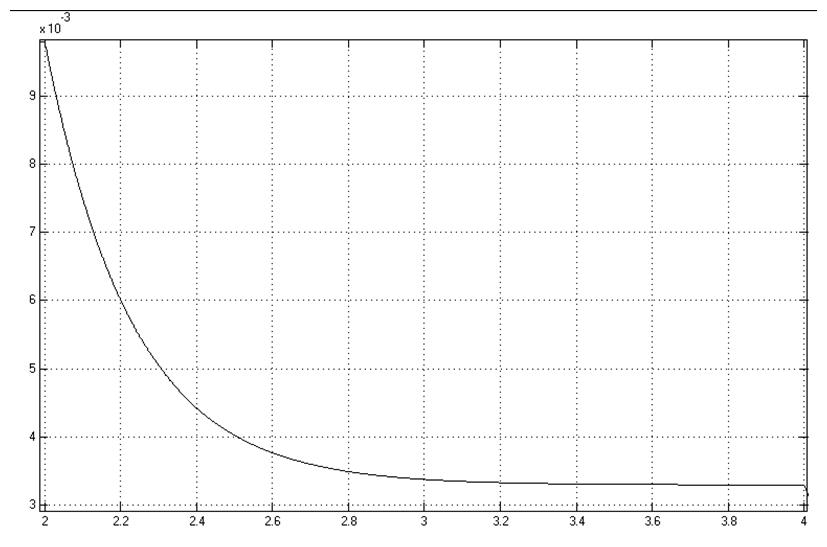 Рис.14(поток генератора)
Рис.14(поток генератора)
|
|||||
|
|||||
|
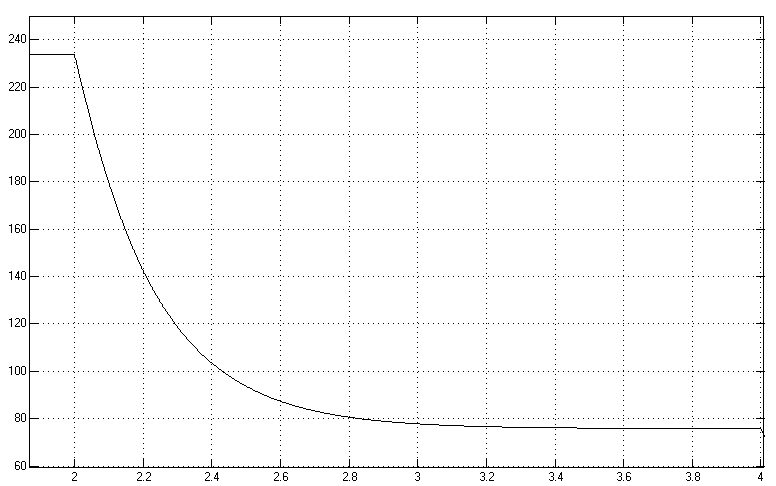 |
Переходные процессы при торможении до нуля
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.