Расчет лестничного марша для общественных зданий ребристой конструкции с фризовыми ступенями и накладными проступями с мозаичным слоем, страница 6

Соответствующие коэффициенты u_s=1,25-_l*_m

От кратковременного действия всей нагрузки

u_s=1,25-1,1*0,31=0,91 < 1

От кратковременного действия постоянной и длительной нагрузок

u_s=1,25-1,1*0,37=0,84 < 1

От длительного действия постоянной и длительной нагрузок

u_s=1,25-0,8*0,37=0,95 < 1

Вычисляем кривизны:

От непродолжительного действия всей нагрузки

1/r₁=M/(h₀*Z)*( u_s/(E_s*A_s)+ +u_b/((u_f+)**E_b*b*h₀))=2212000/(30*26,7)*((0,91/(2*105*3,08)+

+0,9((1,155+0,113)*0,45*2,05*104*9,5*30))=48,31*10^-6 см^-1

от непродолжительного действия постоянной и длительной нагрузок

1/r₂=1175000/(30*26,7)*((0,84/2*105*3,08)+0,9((1,155+0,12)*0,45*2,05*104*9,5*30))=

=23,64*10^-6 см^-1

от продолжительного действия постоянной и длительной нагрузок

1/r₃=1175000/(30*26,7)*((0,95/2*105*3,08)+0,9((1,23+0,113)*0,15*2,05*104*9,5*30))=

=33,51*10^-6 см^-1

Полная кривизна

1/r=1/r₁-1/r₂+1/r₃=(48,31-23,64+33,51)*10-6=58,18*10^-6 см^-1

Прогиб марша

f=1/r*s*l²=58,18*10^-6*5/48*2952=0,53 см и его относительная величина f/l=0,53/295=1/556 < 1/200, т.е. допустима.

При проверке зыбкости от непродолжительного действия груза 1000 Н вычисляют:

Изгибающий момент

M=M_n+N*l₀/4=22120+1000*2,95/4=22857,5 Н*м

Коэффициент _m=2285750/(9,5*302*11*100)=0,243

Относительную высоту сжатой зоны

=1/(1,8+5*(0,243+1,02)/(10*0,0108*9,52))=0,126

Плечо внутренней пары сил

Z=30*(1-(7/30*1,155+0,1262)/(2*(1,155+0,126))=26,6 см

Коэффициент _m=1,15*5921/22857,5=0,30

Коэффициент u_s=1,25-1,1*0,3=0,92 < 1

Кривизна от дополнительного груза  N=1000 Н, вызывающего изгибающий момент

M=N*l₀/4=1000*2,95/4= 737,5 Н*м

1/r=73750/(30*26,7)*((0,92/2*105*3,08)+0,9((1,155+0,126)*0,45*2,05*104*9,5*30))=

=16,21*10^-6 см^-1

и прогиб от этого груза

f=1/r*s*l₀²=16,21*10-6/12*2,952=0,12 см < 0,7 см.

Зыбкость допустима.

3.3.7. Расчёт пристенного продольного ребра

Расчётный пролёт пристенного продольного ребра такой же, как и лобового, т.е. l₀=2,95 м.

Сечение ребра имеет тавровую форму, его размеры: b=11см, h=20см, h_f’=7см, b_f’=0,5*88,5+11,5=56 см.

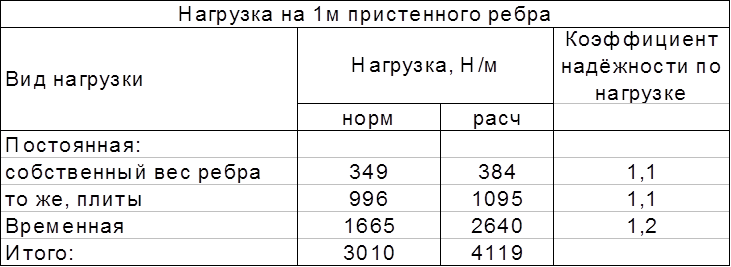
Расчётный изгибающий момент  M=4119*2,95²/8-(1095+2640)*0,55²/6=4317 Н*м

Расчётная поперечная сила Q=0,5*4119*2,95-(1095+2640)*0,55*0,5=5088 Н.

Для расчёта по прочности сечения, нормального к продольной оси элемента, принимают а=2,5 см и вычисляют h₀=20-2,5=17,5 см.

Так как M_f=R_b*b_f’*h_f’*(h₀-0,5*h_f’)=7,65*56*7*(17,5-0,5*7)*100=4198320 Н*см=

=41983,2 Н*м > M=4317 Н*м, то нейтральная ось проходит в пределах полки и сечение рассматривают как прямоугольное шириной b_f’=56 см.

По A₀=M/(b_f’*h₀²*R_b)=431700/(56*17,5²*7,65*100)=0,033 < A_R=0,441 находим =0,033.

Тогда требуемая площадь сечения арматуры A_s=*b_f’*h₀*R_b/R_s=0,033*56*17,5*7,65/365=0,68 см², A_smin=0,0005*11*17,5=0,96 см².

Принимают d12 AIII, As=1,13 cм²

Условие Q=5088 Н < 0,6*0,68*11*17,5*(1+0)*100=7850 Н соблюдается, следовательно, расчёт по прочности сечений, наклонных к продольной оси элемента, на поперечную арматуру не требуется. Поперечную арматуру назначают по конструктивным соображениям, принимая d=5 мм и S=100 мм на приопорных участках и S=200 мм в средней части длины ребра.

Литература

1. СНиП 2.03.01-84*. – Бетонные  и железобетонные конструкции / Госстрой России. - М.: ГУП  ЦПП, 1998.
2. СНиП 2.01.07-85. Нагрузки и воздействия / Госстрой СССР–М.: ЦИТП Госстроя СССР, 1989.
3. Дроздов П.Ф., Додонов М.И., Паньшин Л.Л., Саруханян Р.Л. Проектирование и расчет многоэтажных  гражданских зданий  и  их  элементов. – М.: Стройиздат, 1986.
4. Проектирование  несущей системы многоэтажного здания и его конструктивных элементов. Учеб. пособие/ М. И. Додонов, А.Ю. Родина, Н.И. Сенин, В.Н. Шпанова; Моск. инж.-строит. ин-т им. Куйбышева. М.:, 1993.