Программирование и основы алгоритмизации: Методические указания для проведения лабораторных работ, страница 5

{c=12;h++;} //Цвет попавшей точки - красный

putpixel(x*50+300,-y*50+200,c);} //Печать точек

s=h/N*16;// Расчет площади

cout <<"\nS="<<s;getch();}

// Подпрограмма функции у1 - окружности

double y1(double x){return sqrt(4-x*x);}

// Подпрогрмма функции у2 - прямой

double y2(double x){return x+2;}

//Подпрограмма функции у3 - параболы

double y3(double x){x=x-2;return x*x-2;}

// подпрограмма промежуточной функции – для вычисления точки пе-//ресечения у1 и у3

double f_y(double x) {double y1(double),y3(double); return y1(x)+y3(x);}

//Подпрограмма вычисления нуля функции методом ½ (подробнее см. в //лаб№1)

double zero(double x1,double x2)

{double sig(double),f_y(double);

double x3,y1,y2,y3,eps=0.0000001;

 A:

 x3=(x1+x2)/2.0;

 y1 = f_y(x1);

 y3 = f_y(x3);

 if (sig(y1)==sig(y3))

if (fabs(y3)<eps) return x3; else x1=x3;

 else

if (fabs(y3)<eps) return x3; else x2=x3;

 goto A;}

//Подпрограмма вычисления знака функции (подробнее см. в лаб№1)

double sig(double arg)

{if (arg<0) return 1.; else return 0.;}

Для разных фигур наиболее приемлемыми могут оказаться разные способы интегрирования, некоторые фигуры, например нижнюю часть окружности между параболой и абсциссой, в данном варианте, удобнее было бы интегрировать по у. В данном примере, интегрирование по х проведено с целью показать, как сложную фигуру, ограниченную большим количеством кривых, можно разбить на несколько более простых.

Варианты заданий

Вариант №1

 

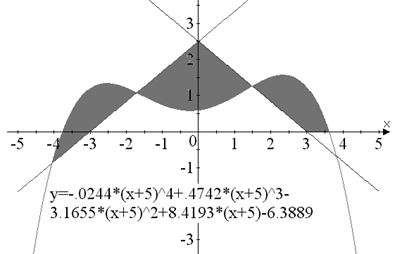Вариант №2

 

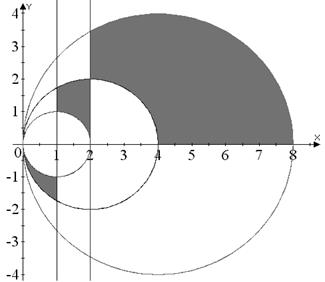Вариант №3

 

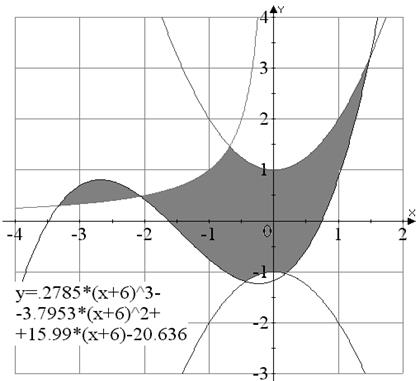Вариант №4

 

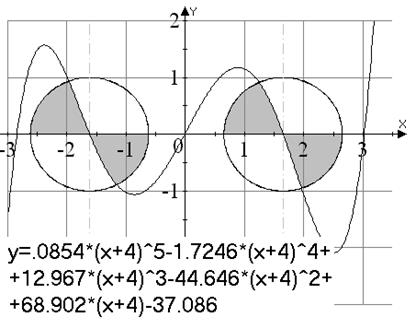Вариант №5

 

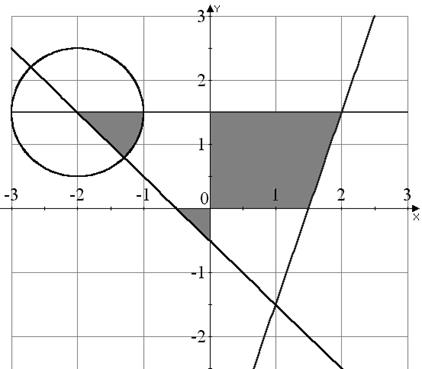Вариант №6

 

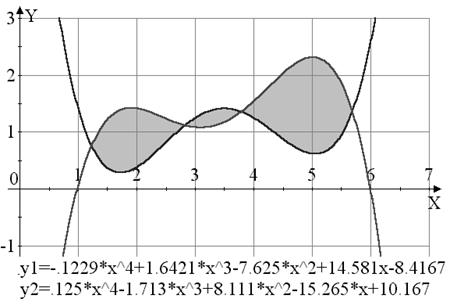Вариант №7

 

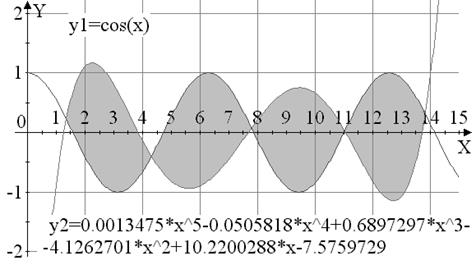Вариант №8

 

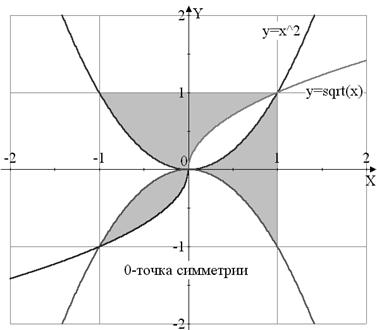Вариант №9

 

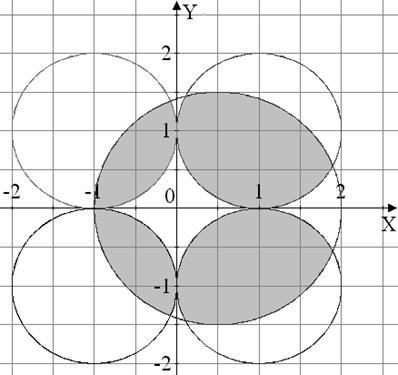Вариант №10

 

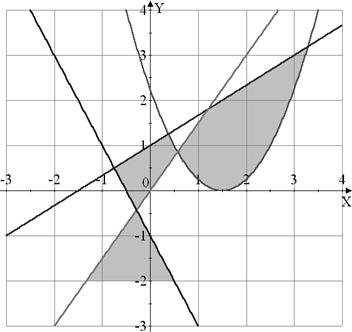Вариант №11

 

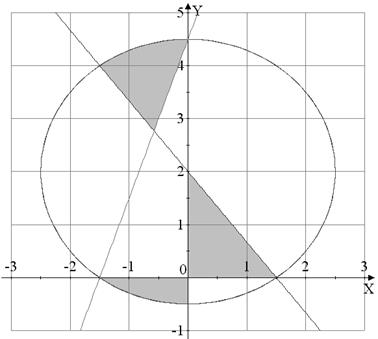Вариант №12

 

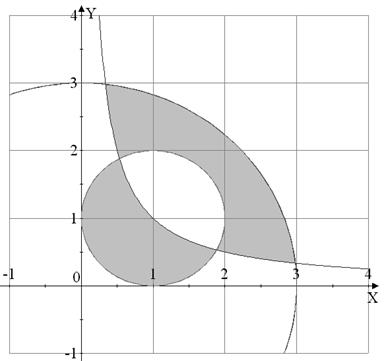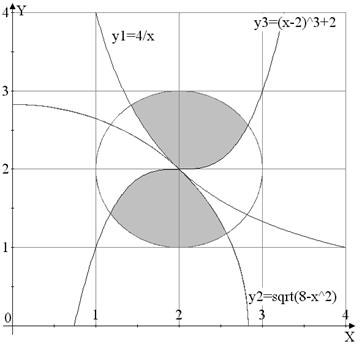Вариант №13

Вариант №14

 

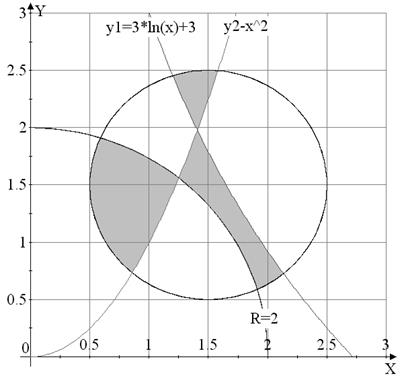Вариант №15

 

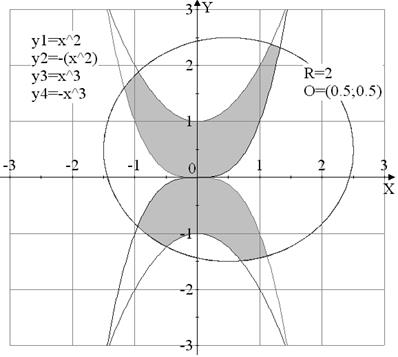Вариант №16

 

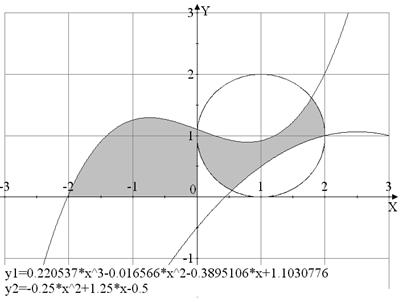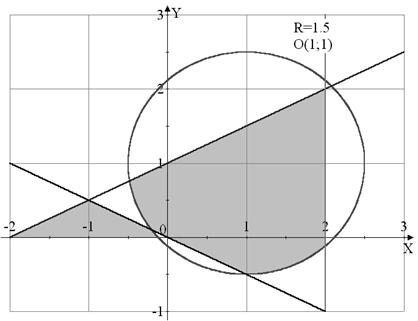
Вариант №17

 

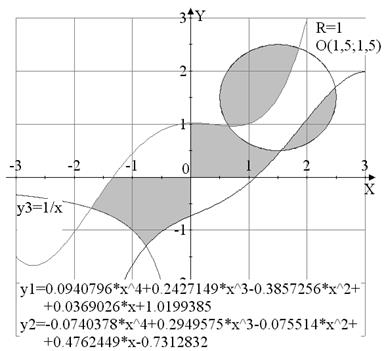Вариант №18

 

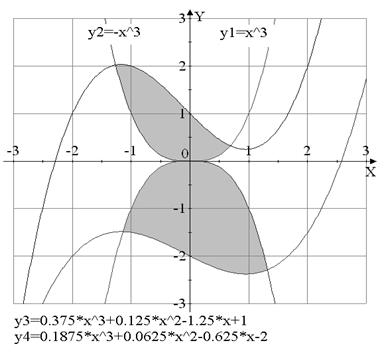Вариант №19

 

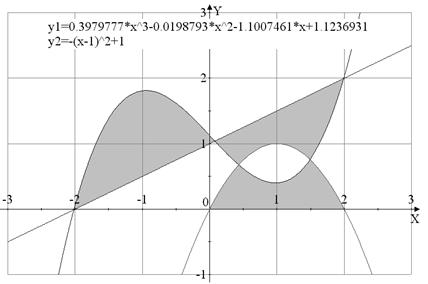Вариант №20

 

ВОПРОСЫ ДЛЯ ЗАЩИТЫ

1.  На защите лабораторных работ 1 и 2, студент должен показать знание языка и среды программирования в пределах лекционного курса.

2.  Особенности реализации методов нахождения нулевых и экстремальных точек математических функций.

3.  Особенности реализации метода трапеций, для сложных областей.

4.  Особенности реализации метода Монте-Карло

5.  Особенности графической иллюстрации математических методов на Языке С++.

СПИСОК ЛИТЕРАТУРЫ

1.  Подбельский В.В. Язык С++: учеб. пособие.- 2-е изд., перераб. и доп. – М.: Финансы и статистика, 1996. 560с. :ил.

2.  Конспект лекций по дисциплине «Программирование и основы алгоритмизации

3.  Программирование и основы алгоритмизации: Метод. указания для курсового проектирования /сост В.С. Ратушняк, Ю.Н. Ратушняк.- Красноярск: КГАЦМ, 2004.- 54 с.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ…………………………………………………………………3

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ……………………………..3

ЛАБОРАТОРНАЯ РАБОТА 1…………………………………………….6

Порядок выполнения……………………………………...………6

Варианты заданий………………………………………………..9

ЛАБОРАТОРНАЯ РАБОТА 2…………………………………………….11

Порядок выполнения……………………………………...………11

Варианты заданий………………………………………………..15

ВОПРОСЫ ДЛЯ ЗАЩИТЫ ……………………………………………….25

СПИСОК ЛИТЕРАТУРЫ………………………………………………….25

СОДЕРЖАНИЕ……………………………………………………………..26