Программирование и основы алгоритмизации: Методические указания для проведения лабораторных работ, страница 3

3. Нахождение нулей выполнять с помощью подпрограмм «метод деления на 2)  с оценкой результата либо по знаку у(х), либо по знаку у’(х)» в зависимости от вида нулевой точки.

Блок-схемы данных алгоритмов представлены на рис.10 и рис.11. ниже.

 

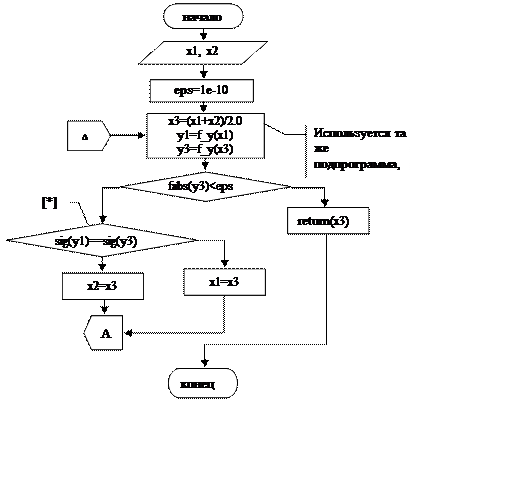[*]- подпрограмма sig – возвращает 0 или 1 в зависимости от знака аргумента.

Рис.10. Метод деления на 2 с оценкой результата по знаку у(х)

 

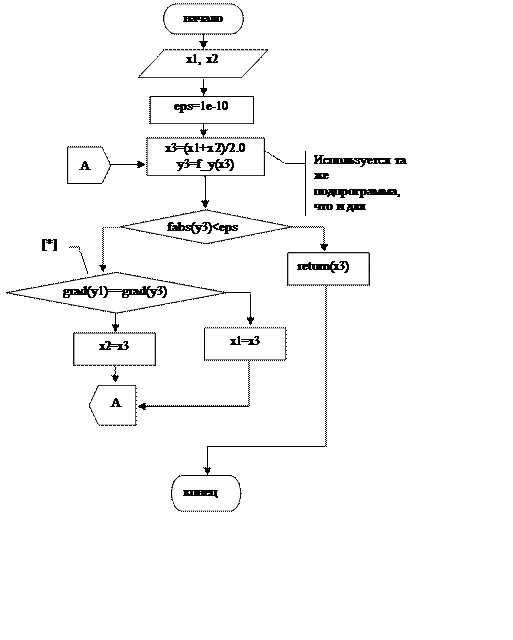[*]- подпрограмма grad – возвращает 0 или 1 в зависимости от знака  производной функции в точке аргумента, в ней используется та же подпрограмма  y(x).

Рис.11. Метод деления на 2 с оценкой результата по знаку у’(х)

В подпрограмме  grad совершенно не обязательно вычислять значение производной – достаточно, задав приращение аргумента - определить ее знак.

Пределы аргументов х1, х2 – в диапазоне которых работают данные алгоритмы легко посмотреть по полученному графику функции – для первой подпрограммы – точки, где функция пересекает абсциссу, для второй – где происходит касание.

Результаты оформляются в виде отдельной таблицы, которая выводится прямо на график, поэтому желательно вывод таблицы нулевых точек вызывать из графического модуля программы до закрытия графического режима приводящего к очистке экрана.

Варианты заданий

1.   в диапазоне [-5;5].

2. 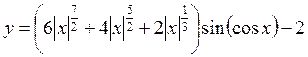  в диапазоне [-0.5;0.5].

3. 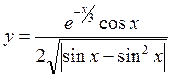  в диапазоне [-9;9].

4. 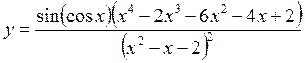  в диапазоне [-3;10].

5. 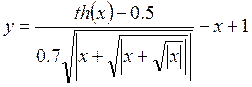  в диапазоне [-1.5;2].

6.   в диапазоне [0;5].

7. 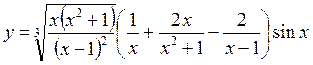  в диапазоне [2;10].

8. 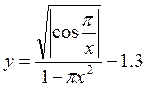  в диапазоне [0.1;0.5].

9. 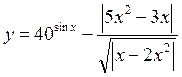  в диапазоне [-20;20].

10. 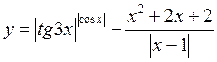  в диапазоне [-3;0.5].

11. 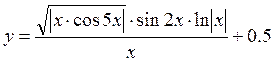  в диапазоне [-0.1;4].

12. 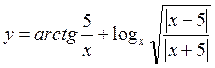  в диапазоне [-10;10].

13. 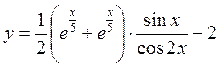  в диапазоне [-4;6].

14. 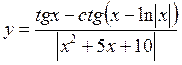  в диапазоне [-5;-0.05].

15. 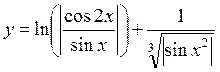  в диапазоне [-0.1;3].

16. 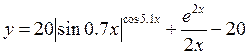  в диапазоне [-3;0].

17. 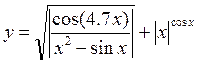  в диапазоне [-1.5;1.5].

18. 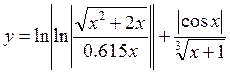  в диапазоне [-1;1].

19.   в диапазоне [0;1].

20. 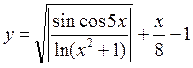  в диапазоне [-2;2].

ЛАБОРАТОРНАЯ РАБОТА 2

Порядок выполнения

В каждом варианте лабораторной работы дана область на координатной плоскости, ограниченная определенными функциями, заданными в различной форме. Задание состоит в следующем:

1. Написать программу расчета площади фигуры на рисунке, двумя способами:

а – последовательного интегрирования (методом трапеций)

б – Монте-Карло.

6. Дополнить алгоритм вычисления площади методом Монте-Карло графической иллюстрацией.

Рассмотрим выполнение работы на примере.

Для примера выполнения задания возьмем такую область(Рис.13.):

 

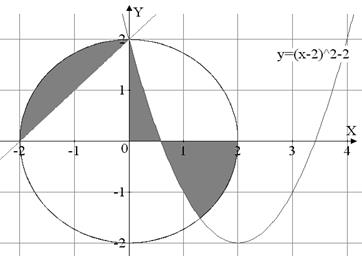Рис.13. Задание примера выполнения работы

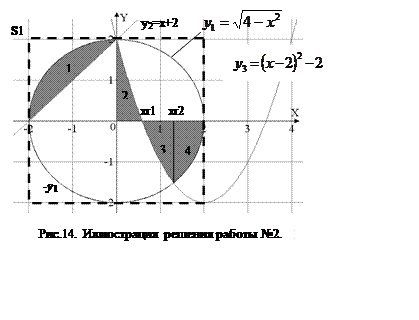
1.  прежде всего определимся сколько фигур и по каким осям мы будем интегрировать (рис.14) а так же сколько функций нам необходимо описать.

Получается 4 фигуры и 4 кривых. Интегрировать все фигуры будем по х. Высота трапеций для фигуры 1 равна разности функций у1 и у2. Для фигуры 2 – равна значению у3. Предел интегрирования 2ой фигуры необходимо вычислить как абсциссу нулевой точки у3 (xr1). Для фигуры 3 так же необходим предел интегрирования (xr2), который является абсциссой точки пересечения у3 и –у1, а высота трапеций равна –у3. Для фигуры 4 высота трапеций равна –(-у1), получается у1.

Сумма всех трапеций в пределах интегрирования дает искомую площадь. При dx стремящемся к 0 – трапеции можно считать прямоугольниками, поэтому их площадь, можно считать как произведение высоты и dx.

Для метода Монте-Карло необходимо условие описания сложной области. Правила написания таких условий:

- сколько кривых ограничивает область, столько отношений связанных (&) будет в описании