- сколько несмежных фрагментов входит в область, столько отношений связанных (or) будет в условии.
Из этого
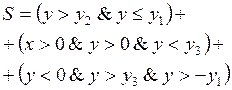
Область расчета S1 «весь ящик с песком» берем квадрат -2:2, как по х так и по у. Чем ближе отношение заштрихованной площади к не заштрихованной приближается к 1 – тем выше точность метода Монте-Карло. Поэтому площадь S1 - рекомендуется не делать ни слишком большой, по отношению к искомой фигуре, но и не слишком малой.
2. Создается проект lab#2
3. Создается файл lab#2.cpp
4. Файл lab#2.cpp подключается к проекту
5. Подключается использование графических библиотек в свойствах линкера.
6. Текст программы:
// Прежде всего при помощи препроцессорных директив подключаем необходимые функции.
#include <iostream.h> // Потоки ввода-вывода
#include <graphics.h> // Работа с графикой
#include <fstream.h> // Работа с файловыми потоками
#include <conio.h> // Работа с терминалом
#include <STDLIB.H> // Работа со строками
#include <stdio.h> // Функции ввода-вывода
#include <math.h> // Математические функции
main() // тело основной программы
//Инициализация графического режима, подразумевается, что файл //egavga.bgi находится в том же каталоге, что и проект
{int dr = DETECT, mod =1;initgraph (&dr,&mod,""); setcolor(15);//Установка цвета – ярко белый
//Проводим оси координат, квадрат 7х7 (так как от-3 до 3 и по х и по у)
for (double i=0;i<8;i++)
//Условие обеспечивает проведение осей координат ярко белым, а вспо//могательных – серым цветом
{if (i==3)setcolor(15);else setcolor(8); line(150,50+50*i,500,50+50*i);
line(150+50*i,50,150+50*i,400);}
//Подключим подпрограммы вычисления всех присутствующих на гра//фике кривых
double y1(double), y2(double), y3(double), zero(double,double);
// xr1 и xr2 – абсциссы точек пересечения кривой с окружностью
// необходимы нам для метода трапеций
double xr1=2-sqrt(2),xr2=zero(0.,2.),x,si,s=0,c;
cout <<"\nx1=-2" <<"\nx2=0"
<<"\nx3="<<xr1
<<"\nx4="<<xr2<<"\nx5=2";
//Вывод графиков в заданных диапазонах
for (i=0;i<350;i++)
{double xg=i+150,yg=200;
x=i*7/350.-3; // Масштабный коэффициент
if (fabs(x)<=2) yg = y1(x)*50+200; putpixel(xg,yg,15);
if (fabs(x)<=2) yg = -y1(x)*50+200; putpixel(xg,yg,15);
if (x<=0&&x>=-2)yg = -y2(x)*50+200; putpixel(xg,yg,15);
if (x>=0&&x<=4) yg = -y3(x)*50+200; putpixel(xg,yg,15);}
cout << "\nМетод #1";
//Метод трапеций заключается в последовательном интегрировании (в //данном случае интегрируется у по х)
c=0.0001;// шаг интегрирования по х
for (x=-2; x<=0; x+=c) {si=(y1(x)-y2(x))*c; s=s+si;}
for (x=0; x<=xr1; x+=c) {si=(y1(x)-y3(x))*c; s=s+si;}
for (x=xr1;x<=xr2;x+=c) {si=-y3(x)*c; s=s+si;}
for (x=xr2; x<=2; x+=c) {si=y1(x)*c; s=s+si;}
//результат
cout <<"\nS="<<s;
cout <<"\nНажмите любую клавишу";getch();
cout << "\nМетод #2 (Монте-Карло)";
double N=1e6,h=0,y;// N – Количество точек «Насыпаемых» в заданную //область
for (i=0;i<=N;i++)
{// вычисление случайных координат «насыпаемых» точек
x=(random(1e4)/1e4)*4.-2.;
y=(random(1e4)/1e4)*4.-2.;
c=10;//цвет не попавшей точки - зеленый
//Условие, описывающее фигуру с искомой площадью
if ((y<=y1(x)&&y>=y2(x)) ||(x>=0&&y>=0&&y<=y3(x)) ||(y<=0&&y>=y3(x)&&y>=-y1(x)))
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.