

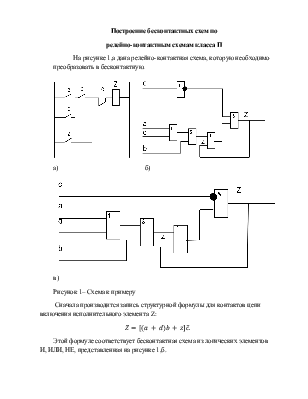





Поэтому схему можно описать несколькими структурными формулами:
X= ab + de + ace + dcb;
X= a(b + ce) + d(e +cb); (1)
X= b(a + dc) + e(d + ac);
X= ab + de + c(ae + db).


а) б)
в) г)

д)
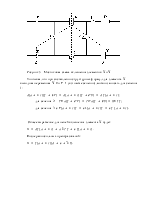
Рисунок 2 - Мостиковая схема класса Н и эквивалентные ей схемы класса П
Все структурные формулы (1) могут быть получены из первой путем равносильных преобразований. Каждой из формул соответствует определенная схема (рисунок 2, б-д). Эти схемы равносильны по действию схеме на рисунок 2,а, но существенно сложнее ее. Число контактов в мостиковой схеме значительно меньше, чем в равносильных ей последовательно-параллельных структурах.
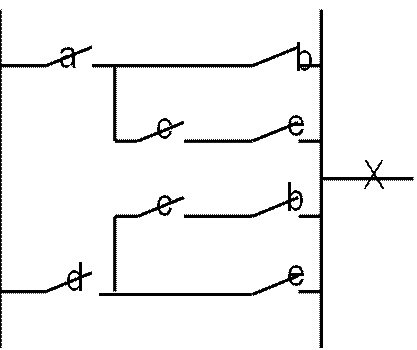
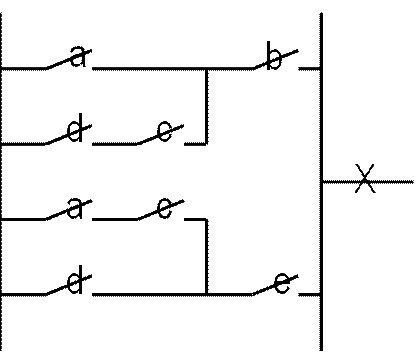
На рисунке 3 приведены бесконтактные схемы, соответствующие контактным схемам на рисунке 2,б,в. Вариант бесконтактной схемы на рисунке 3,а содержит меньше элементов.


а) б)
Рисунок 3 - Бесконтактные схемы, эквивалентные схемам б и в на рисунке 2
Таким образом, при построении бесконтактной схемы по релейно-контактной схеме, содержащей узлы с мостиковыми соединениями контактов (схема класса Н), необходимо привести эти схемы к эквивалентным схемам последовательно-параллельной структуры (схемы класса П).
Существует несколько методов решения указанной задачи.
1. Метод выделения цепей, проходящих через начальные или конечные элементы
На рисунке 4,а представлена исходная релейно-контактная мостиковая схема. Разложение может быть произведено как по начальным, так и по конечным элементам схемы. В качестве начальных элементов могут быть приняты, например, элементы a и b, а в качестве конечных – элементы g и x.


а) б)

в)
Рисунок 4 - Пример разложения мостиковой схемы по начальным элементам
Для получения последовательно-параллельной структуры, по которой могут быть составлены структурные формулы, например для элементов X и Y, можно разложить исходную схему (рисунок 4,а) по начальным элементам так, как это показано на рисунок 4,б. На этой схеме вычерчены отдельные цепи питания элементов X и Y.
Так как в схеме все еще имеются мостиковые соединения, то ее следует снова разложить по начальным элементам. В данном случае элементы d и f будут начальными элементами для цепи элемента X, а e и f – для цепи элемента Y.
Полученная в результате разложения схема представлена на рисунок 4, в. Как видно из рисунков, при разложении схемы по начальным элементам получается столько параллельных цепей, сколько имеется в схеме начальных элементов. Каждая параллельная цепь строится для одного начального элемента; в местах включения других начальных элементов в цепи делаются разрывы.
При разложении схемы по конечным элементам производятся те же операции, только с другого полюса схемы.
По схеме на рисунок 4,в можно записать структурные формулы, необходимые для построения бесконтактной схемы:
![]() ;
;
![]() .
.
2. Метод записи структурных формул для всех возможных цепей включения элементов
Этот метод был применен к схеме на рисунке 2,а. Применение этого метода к схеме на рисунке 4,а для всех возможных цепей включения элементов X и Y и выполнение равносильных преобразований полученных структурных формул приводит к следующим выражениям:
![]()
=![]() ;
;
![]()
![]() .
.
Полученные формулы одинаковы с найденными первым методом.
3. Метод «сечений»
Для выявления цепей включения элемента, расположенного в середине схемы, целесообразно пользоваться методом «сечений». По этому методу через рассматриваемый элемент проводятся все возможные сечения схемы. Для каждого сечения записывается алгебраическое выражение включения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.