линейных электрических цепях свободные составляющие токов и напряжений затухают во времени по показательному закону ept
Из трех токов (полного, принужденного и свободного) основое значение имеет полный ток. Полный ток является тем током , который в действительности протекает по той или иной ветви цепи при переходном процессе. Его можно измерить и записать на осциллограмме .
1 закон коммутации.
2 закон коммутации.
 |
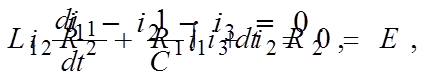 |
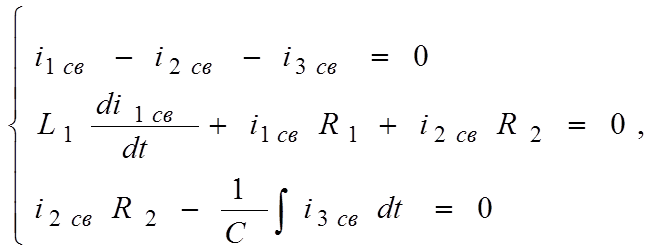 |
|||
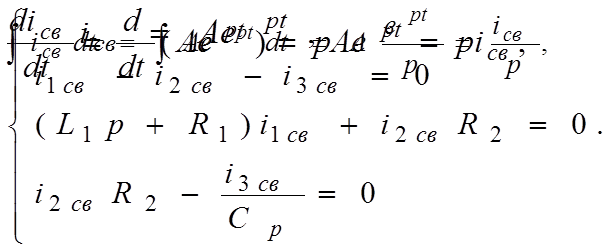 |
|||
Это уравнение представляет собой систему алгебраических уравнений и не
содержит производных и интегралов.
Переход от систему дифференциальных уравнений к системе алгебраических уравнений из алгебраизацией системы дифференциальных уравнений.
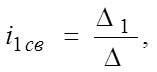 |
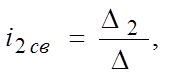 |
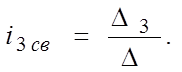 |
|||
D
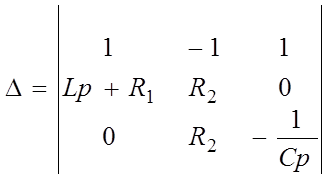 |
D1 получают из определителя системы D путем замены первого столбца правой частью уравнения 5.
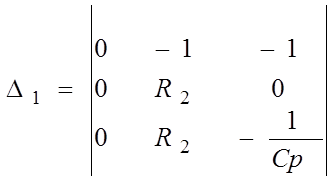 |
D2 получают из D путем замены второго столбца правой частью системы (5). Если в определителе один из столбцов состоит из нулей, то D1=0, D2 =0, D3=0.
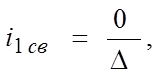 |
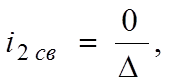 |
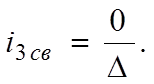 |
|||
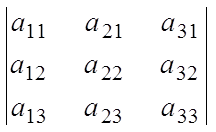 |
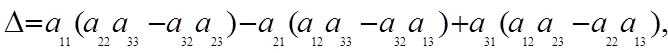 |
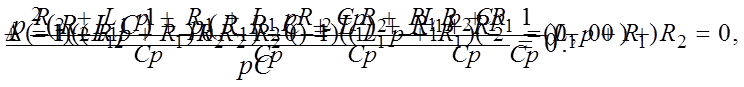 |
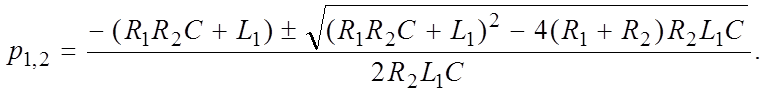 |
Говорилось, что iсв=Aept.
Если характеристическое уравнение будет иметь не один корень, а несколько, например n, то для каждого свободного тока нужно взять
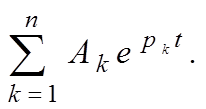 |
Характеристическое уравнение для определения p часто составляют более простым путем. С этой целью составляют выражение входного сопротивления для любой ветви цепи на переменном токе z(jw), заменяют в нем jw на p и приравнивают z(p) и нулю.
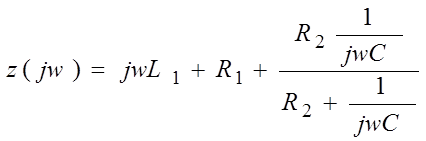 |
Jw=p и равен 0
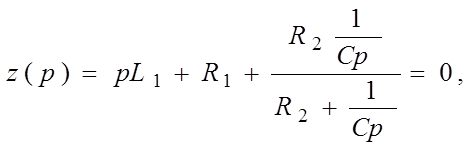 |
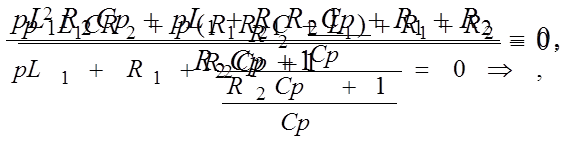 |
Число корней характеристического уравнения = степени этого уравнения.
Уравнение 1 степени имеет всегда отрицательный действительный корень.
Уравнение 2 степени может иметь:
а) 2 действит. неравных отрицат. корня;
б) 2 действит. равных отрицат. корня;
в) 2 комплексно сопр. корня с отрицат. действит. частью.
Уравнение 3 степени может иметь:
а) 3 действит. неравных отрицат. корня;
б) 3 действит. отрицат. корня, из которых 2 равны друг другу;
в) 3 действит. равных отрицат. корня;
г) 1 действит. отрицат. корень и 2 сопряж. с отрицат. действит. частью.
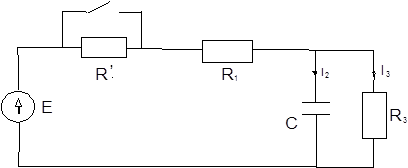 |
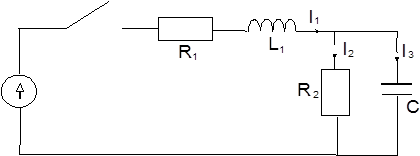
Требуется: 1) найти полные, принужденные и свободные составляющие токов и напряжения на конденсаторе j, 2) определить токи i1, i2,i3 и напряжение Uc в фунции времени.
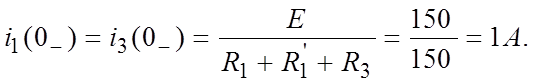 |
|||
Принужденные значения после коммутации:
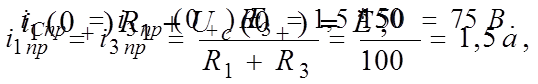 |
|||
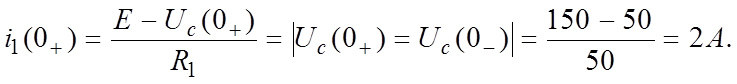
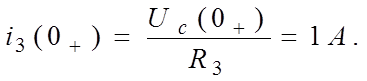 |
![]()
По первому закону Кирхгофа
Свободные составляющие найдем как разности между полными и принужденными составляющими.
Характеристическое уравнение схемы
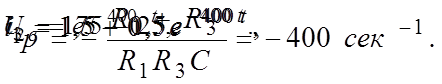 |
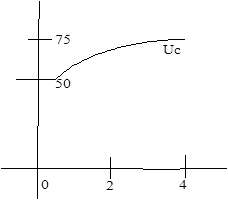 |
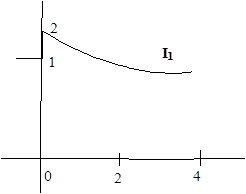 |
||
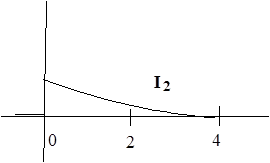 |
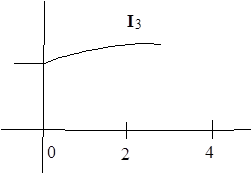 |
||
Преобразование Лапласа.
Переход от фунции времени и фунции p осуществляется с помощью преобразования Лапласа. Операторный метод расчета позвооляет свести операцию дифференцирования к умножения, а операцию интегрирования - к делению.
Условимся под понимать комплексное число p=a+jb
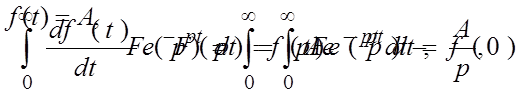 |
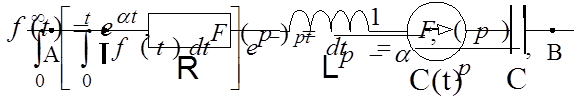 |
Выразим потенциал точки A через потенциал точки B.
Вместо , вместо
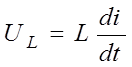 |
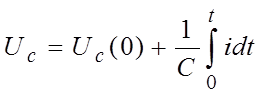 |
||
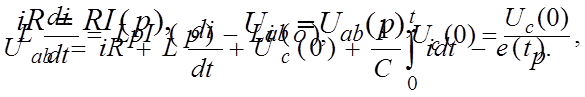 |
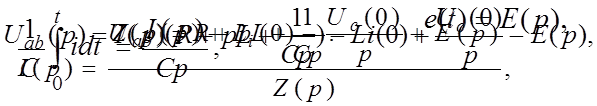 |
Z(p) представляет собой операторное сопротивление участка цепи
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.