Аппроксимация характеристик нелинейных элементов

Аппроксимация характеристик нелинейных элементов

Как правило, ВАХ нелинейных элементов получают экспериментально; реже удается найти их из теоретического анализа. Для исследования необходимо подобрать функцию аппроксимации такую, которая, будучи довольно простой, отражала бы все возможные особенности экспериментальной снятой характеристики с достаточной степенью точности. Чаще всего используют следующие способы аппроксимации вольт-амперных характеристик двухполюсников: кусочно-линейная, степенная, показательная аппроксимация.

Кусочно-линейная аппроксимация

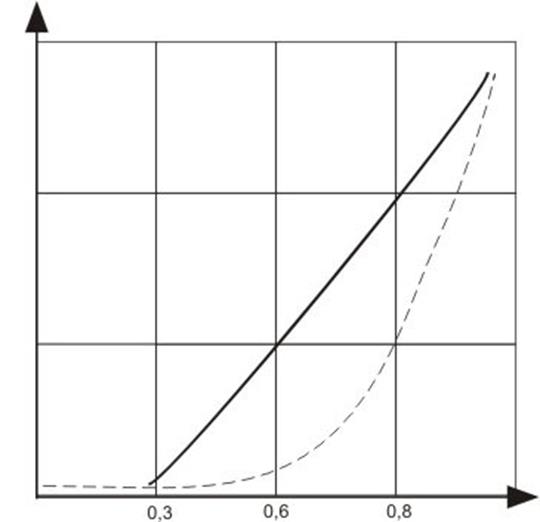
Такую аппроксимацию обычно применяют при рассчете процессов в нелинейных уравнениях в случае больших амплитуд внешних воздействий. Данный способ основан на апроксимации характеристик нелинейных элементов, т.е. на приближенной замене реальной характеристики отрезками прямых линий с различными наклонами. На рисунке показана входная характеристика реального транзистора, аппроксимированная двумя отрезками прямых.

Аппроксимация определяется двумя параметрами – напряжением начала характеристики Uн и крутизной S. Математическая форма аппроксимированной ВАХ такова:

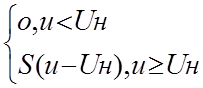
Напряжение начала входных характеристик биполярных транзисторов имеет порядок 0,2-0,8 В: крутизна характеристики тока базы iб(Uбэ) около 10мА/В. Крутизна характеристики iк(Uбэ) тока коллектора в зависимости от напряжения база-эмиттер, то величина 10мА/В должна быть умножена на h21э – коэффициент усиления тока базы. Поскольку h21э =  100-200, указанная крутизна имеет порядок нескольких ампер на вольт.

Степенная аппроксимация

Степенную аппроксимацию широко используют при анализе работы нелинейных устройств, на которые подаются относительно малые внешние воздействия. Этот способ основан на разложении нелинейной вольт-амперной характеристики i(u)  в ряд Тейлора, сходящийся в окрестности рабочей точки U0.

i(u) =

количество членов разложения зависит от заданной точности. Рассмотрим пример:

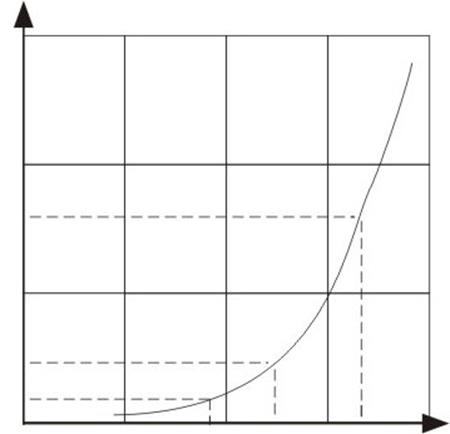
                                0,5        0,7         0,9                

Входная характеристика транзистора. Рабочая точка U0=0,7В. Выбираем в качестве узлов аппроксимации точки 0,5; 0,7 и 0,9 В.

Необходимо решить систему уравнений :

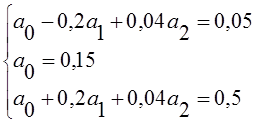
Спектральный состав тока в нелинейном элементе при внешнем гармоническом воздействии

Рассмотрим цепь, состоящую из последовательного соединения источника гармонического сигнала Uс(t) = coswt, источника постоянного напряжения смещения U0 и безинерционного нелинейного элемента. Для этого рассмотрим рисунок.

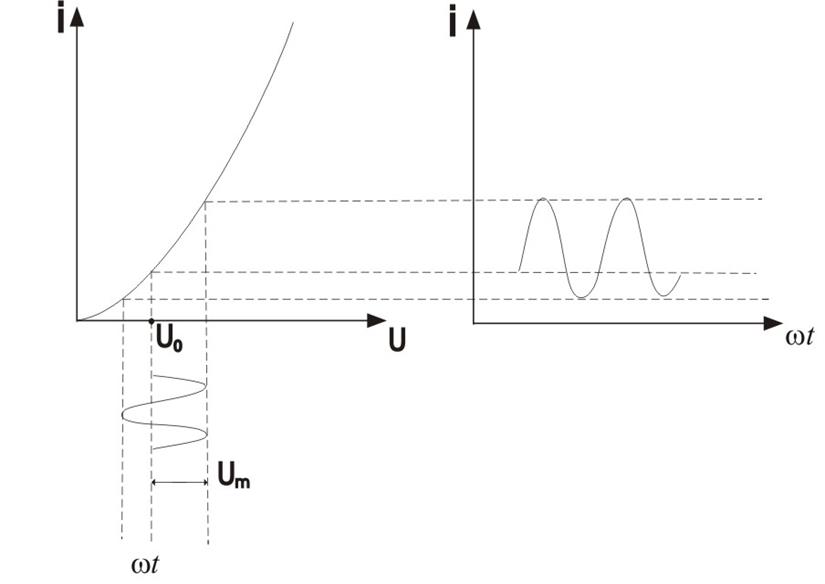
Ток в цепи имеет синусоидальную форму.

Форма тока и напряжения оказываются различными.

Причина искажения кривой тока проста: одинаковым приращениям напряжения отвечают неодинаковые приращения тока, т.к.  , а дифференциальная крутизна ВАХ на разных участках различна.

Рассмотрим задачу аналитически.

Пусть нам известна нелинейная функция i(u)=i(Uc,U0). На нелинейный элемент действует напряжение сигнала Uc(t)=Umcos(wt+j).

Безразмерная величина x=wt+j, тогда I(x)=I(Umcosx, U0) – переодическая функция относительно аргумента x с периодом 2T. Представим ее рядом Фурье 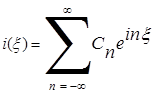 с коэффициентами  .

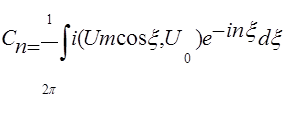Функция i(x) четная, поэтому ряд Фурье будет содержать только косинусные составляющие: .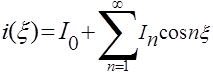

Амплитудные коэффициенты гармонии

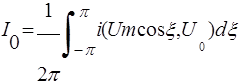
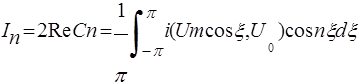
n=1,2,…

Две последние формулы дают общее решение задачи о спектре тока в нелинейном элементе при гармоническом внешнем воздействии:

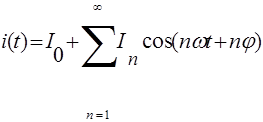
т.е. ток, кроме постоянной составляющей I0, содержит бесконечную последовательность гармонии с амплитудами In. Амплитуды гармонии зависят от параметров Um и U0, а также от вида аппроксимирующей функции.

Рассмотрим каким образом зависит от вида аппроксимирующей функции.

Кусочно-линейная

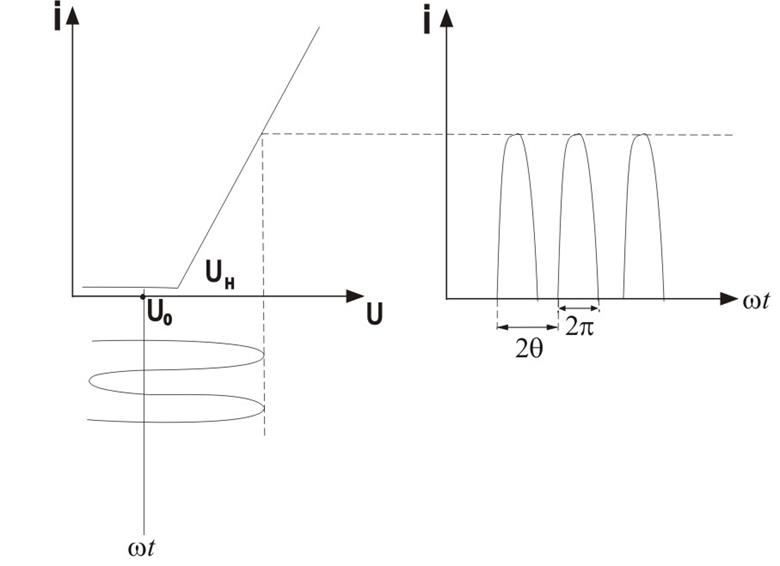
i(U)=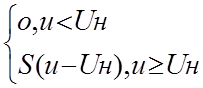

Подано напряжение u(t)=U0+Umcoswt.

График тока имеет вид косинусоидальных импульсов с отсечкой. Угол отсечки импульсов тока определяется из равенства:

U0+Umcosq=Uн Þ .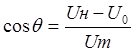

Степенная аппроксимация.

Пусть в окрестности рабочей точки U0 ВАХ нелинейного элемента