Обработка результатов прямых многократных равноточных измерений: Методические указания к выполнению контрольной работы по дисциплинам "Метрология, стандартизация и технические измерения" и "Метрология, стандартизация и управление качеством", страница 7

При m<4 пользуются формулой

.

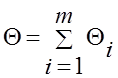К п.3.10

Суммарная погрешность результата складывается из случайной составляющей  и неисключенной суммарной систематической погрешности . Если отношение  меньше 0.8, то неисключенной систематической погрешностью пренебрегают и в качестве границы погрешности результата измерения принимают . Если , то принебрегают случайной погрешностью и . Если , то учитывают систематическую и случайную погрешности:

.

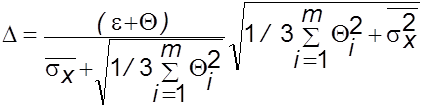С погрешностью не более 10% эта формула заменяется более простой:

,

которая считается универсальной для всех видов измерений.

К п.3.11

Существуют следующие формы представления результатов:

1)  в виде  - для симметричного доверительного интервала;

2)   - для несимметричного доверительного интервала;

3)   - если функции распределений составляющих погрешностей неизвестны.

Погрешность выражается числом с одной цифрой, если цифра старшего разряда больше трех, или двумя значащими цифрами, если цифра старшего разряда равна трем или меньше трех. А также в случае более точных измерений. Оценка измеряемой величины  должна быть записана числом , оканчивающимся цифрой того же разряда, что и интервальная оценка. Поэтому необходимо провести округление результатов по следующему правилу:

·  если первая из отбрасываемых цифр больше или равна 5, а за ней есть еще значащие цифры, то последнюю из сохраняемых цифр увеличивают на 1. Например: 28,754 - 28,8;

·  если отбрасываемая цифра 5, а за ней нет значащих цифр, то последнюю сохраняемую цифру оставляют неизменной, если она четная, и увеличиваю на 1, если она нечетная, Например: 28,75 - 28,8; 28.65 - 28.6;

·  если первая из отбрасываемых цифр меньше 5, последнюю сохраняемую цифру не изменяют, Например:218,74 - 218,7.

Округление производится лишь в окончательном ответе, а все предварительные расчеты выполняются не менее, чем с одним лишним знаком.

ЛИТЕРАТУРА

1.Елизаров А.С. Электрорадиоизмерения: Учебник для вузов по специальности "Радиотехника". - Минск: Вышейшая школа,1986.

2.Дворяшин Б.В. Основы метрологии и радиоизмерения: Учебное пособие для вузов. - М.: Радио и связь,1993.

3.Винокуров В.И., Каплин С.И., Петелин И.Г. Электрорадиоизмерения: Учебное пособие для радиотехнических специальностей вузов / Под ред. Винокурова В.И. - М: Высшая школа, 1986.

4.Алиев Т.М. Тер- Хачатуров. Измерительная техника: Учебное пособие для технических вузов. - М.: Высшая школа, 1991.

5.Методические указания к расчетно-графическим работам по курсу "Электрорадиоизмерения" /Авт.-сост.: Р.А.Ибатуллин, Н.А.Миляев.-М.: Изд-во МАИ, 1988.

Приложение 1

Табулированная функция Лапласса