Обработка результатов прямых многократных равноточных измерений: Методические указания к выполнению контрольной работы по дисциплинам "Метрология, стандартизация и технические измерения" и "Метрология, стандартизация и управление качеством", страница 6

В таблице 3 - количество интервалов . Если n<200, то обычно принимают . Необходимо, чтобы каждый интервал содержал не менее 5 наблюдений, в противном случае малочисленные интервалы объединяют, суммируя их частоты. Если результат наблюдения находится точно на границе двух интервалов, то условно считается, что данное значение принадлежит в равной мере обоим интервалам, и поэтому необходимо прибавлять к величинам m каждого интервала по 0,5.

Теоретическая вероятность попадания результатов  в каждый интервал определяется по формуле

,

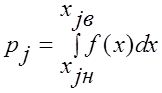где xjн и xjв - соответственно нижняя и верхняя и границы j-го интервала; f(x) - теоретическая плотность распределения вероятностей, которой сглажена гистограмма.

Для нормального закона распределения вычисления  можно упростить, пользуясь формулой

,

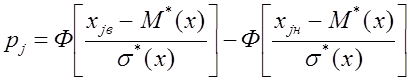
где Ф (Z)- табулированная функция Лапласа. Ее значения для различных значений аргумента 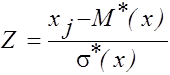 приведены в приложении 1.

После этого вычисляется значение :

.

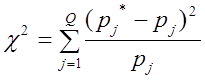Затем по таблице критических точек распределения  находят критическую точку  от заданного уровня значимости g и числа степеней свободы  (приложение 2). Далее сравнивают полученные результаты. Если , то гипотезу принимают, если , то отвергают.

Составной критерий о принадлежности результатов наблюденийнормальному распределениювсоответствии с ГОСТ    состоит из двух критериев.

Критерий 1.По результатам наблюдений вычислить отношение

,

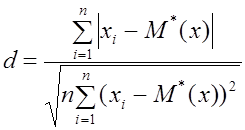проверить условие

,

где  и - процентные точки(квантили) распределения величины , получаемые из таблицы (см. приложение 3) для заранее выбранного уровня значимости  и количества наблюдений . Если условие выполняется, то гипотеза о нормальности распределения по критерию 1 не отвергается, в противном случае гипотеза отвергается.

Критерий 2. Этот критерий введен дополнительно для проверки "концов" распределения. Гипотеза о нормальности распределения по критерию 2 принимается, если количество разностей  превосходящих , будет не более , где r - число степеней свободы(см. метод. указания к п 3.7);  - верхняя квантиль(процентная точка ) нормированной функции Лапласа, соответствующая вероятности P, которая определяется по таблице (приложение 5) по выбранному уровню значимости  и числу наблюдений .

Если число разностей , больших , превышает , то гипотеза отвергается.

Гипотеза о нормальности распределения по составному критерию принимается, если выполняются оба критерия. Результирующий уровень значимости составного критерия

.

Величина  устанавливается в пределах от 2% до 10%.

К п.3.8

Доверительный интервал определяется как

,

где t - коэффициент, зависящий от доверительной вероятности Р и объема выборки.

При заданной вероятности P величину t определяют законом распределения. Для определения доверительного интервала доверительную вероятность Р принимают равной 0,95. В случаях когда измерения повторить нельзя, и они связаны с созданием эталонов и здоровья людей, Р=0,99.

Для нормального закона при  коэффициент t выбирается по таблицам Лапласа (для P=0,95 t=2,01), при  в качестве t берется коэффициент распределения Стьюдента (приложение 4) Тогда интервал определяется как

.

К п.3.9.

Определяются границы неисключенной систематической погрешности

,

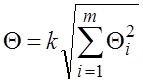где - границы i-й неисключенной систематической погрешности; m-число измеряемых погрешностей; к – коэффициент, зависящий от доверительной вероятности, при Р=0.95 к=1,1.