Аналитическое определение и графическое изображение скорости, нормального, касательного и полного ускорения точки

Задача № 1.

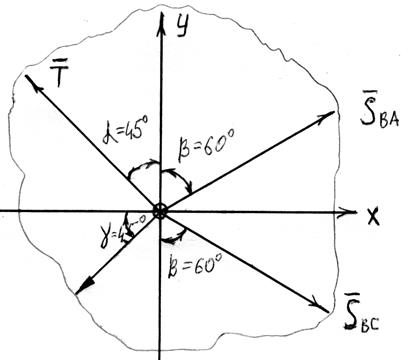
            Определить реакции гладких связей и усилия в стержнях кронштейна АВС.

Если: P = 4 кН; Q = 2 кН; α = 45º; β = 60º; γ = 45º.

 

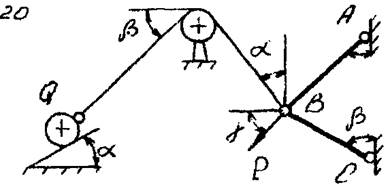 Дано:                                                                                                                                       

 

P = 4 кН

Q = 2 кН

α = 45º

β = 60º

γ = 45º

Т - ?

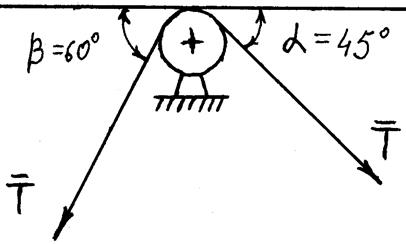
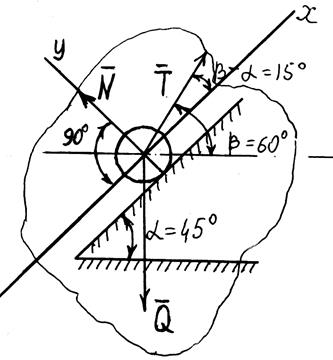S_BA - ?                1)Определяем усилие (Т) в тяге, удерживающей каток весом Q на наклонной

S_BС - ?                плоскости из условия равновесия сходящейся системы сил:

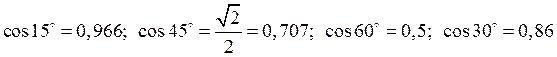
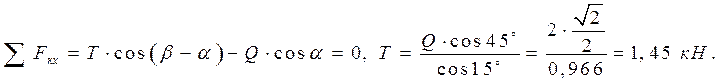2) Определяем усилия в стержнях  из условий равновесия сходящейся системы сил:

Решаем систему уравнений.

Умножим 2) на 1,72 и складываем.

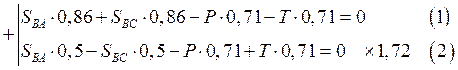
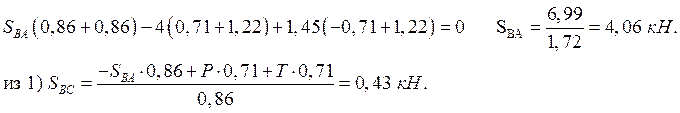
Ответ:

Задача № 2.

            Определить реакции связей в конструкции, схема которой приведена на рисунке.

Если: P = 60 кН; q = 20 кН / м; К = 5; а = 0,5 м; α = 30º.

 

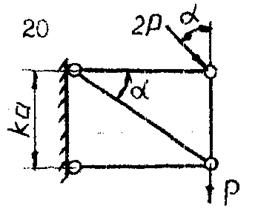 Дано:                                                                                                                                      

 

P = 60 кН

q = 20 кН / м

К = 5

а = 0,5 м

α = 30º

N_АС - ?

N_АВ - ?                          Определяем усилия в стержнях конструкции способом вырезания

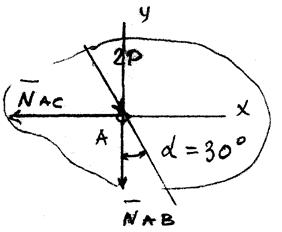N_ВС - ?                           узлов: sin30º=0,5; cos30º=0,86; cos60º=0,5.

N_ВД - ?

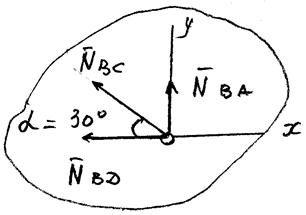
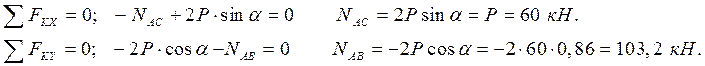
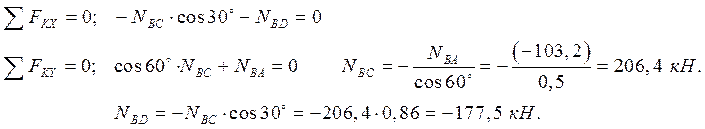
Знак минус для усилий  означает противоположное направление на рисунках т. е. сжатие.

Ответ:

Задача № 3.

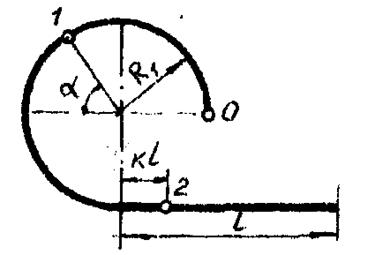
            Движение точки задано уравнением S = n · t², где S - расстояние в метрах, отсчитывается от точки О, t- время в секундах. Траектория движения изображена на рисунке. Определить аналитически и изобразить в масштабе графически скорость, нормальное, касательное и полное ускорение точки в положении 1, 2 на траектории.

Если: n = 0.4 м · с²; l = 4 м; R₁ = 4 м; R₂ = 2 м; К = 0,8; α, _град. = π / 3.

 Дано:                                                                                                                                       

 

n = 0.4 м · с²

l = 4 м

R₁ = 4 м

R₂ = 2 м

К = 0,8

α, _град. = π / 3

 

v-?;      а_n-?; 

а -?;     а_ד-?.

1)  Определяем длину пути, пройденной до:

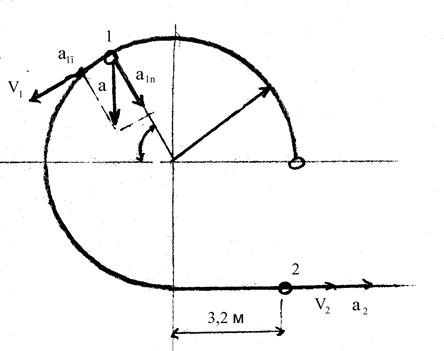положения 1.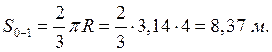     

положения 2.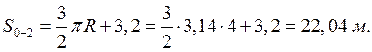     

2)  Время пути до:

точки 1.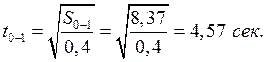              

точки 2.              

3)  Скорость точки: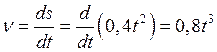

4)  Ускорение касательное: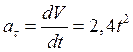

      Ускорение нормальное: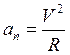

Для положения точки 1: 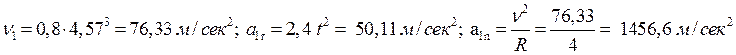 Полное ускорение:

Для положения точки 2: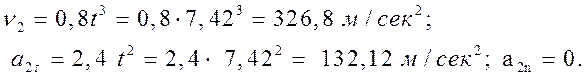

Ответ:

Задача № 4.

            Подобрать прочные размеры двух вариантов поперечных сечений упругих элементов конструкций, схемы которых изображены на рисунке. Заштрихованные элементы считать абсолютно жесткими. Упругие стержни – стальные. Принять [σ] = 160 МПа; а = 1 м; Р = nqa; q = 30 кН / м; К = 3; n = 5; α = 30º.

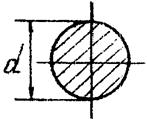
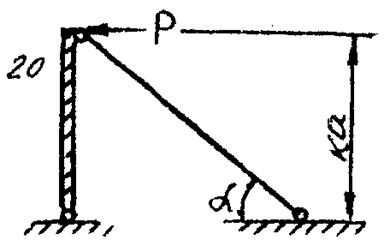
 Дано:                                                                                                                                       

[σ] = 160 МПа

а = 1 м

Р = nqa

q = 30 кН / м

К = 3

n = 5

α = 30º

 

d-?; А₁-?; А₂-?.

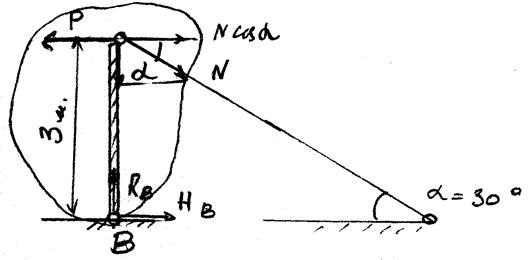            Определяем усилие в стержне N из условия равновесия относительно точки В.

Рассматриваем равновесие плоской системы сил. (сos30º=0,86)                  

 

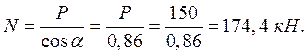
Условия прочности при растяжении – сжатии:

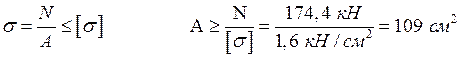
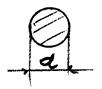Для круглого сечения:

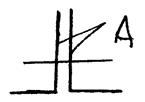
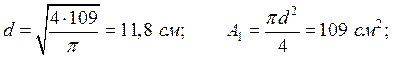
Для уголка (ГОСТ 8510 – 72), LN 25/16☓16, А₂=2☓63,6=127,2 см².

Ответ:

Задача № 5.

            Для балок, схемы которых изображены на рисунке, построить эпюры поперечных сил и изгибающих моментов. Подобрать прочные размеры для круглого сечения диаметром d и прямоугольного с соотношением сторон h = 3b, где h - высота, b - ширина сечения. Полученные результаты сопоставить по расходу материала (весу или материалоемкости) и определить рациональную форму сечения. Принять материал - титан технический: n_т = 2,  = 520 МПа. Здесь n_т - коэффициент запаса по текучести, σ _тр и σ _тс - пределы текучести материала на растяжение и сжатие. Если: l = 0,5 м; Р = 2 кН; М = 2 кН·м; К = 3.