
Частотные характеристики разомкнутой ИС
Передаточная функция разомкнутой ИС является передаточной функцией с периодом 2π.
Это объясняется следующим:
дискретная передаточная функция разомкнутой ИС является функцией параметра z, где z параметр дискретного преобразования Лапласа.
Из подстановки z= eq и q= jω получаем ejω или ejω=cosω+jsinω,
где cosω и jsinω периодические функции с периодом 2π.
Следовательно, при построении ЧХ ИС достаточно рассматривать интервал частот от - π до π, а учитывая, что P(ω) четная функция, а Q(ω) – нечетная, можно ограничиться интервалом от 0 до π.
Частотная характеристика – это реакция звена (системы) на гармоническое типовое воздействие.
Будем считать, что на вход подается сигнал вида ![]()
где ![]() – амплитуда гармонического
воздействия от генератора гармонических сигналов,
– амплитуда гармонического
воздействия от генератора гармонических сигналов, ![]() и
и ![]() считаются известными.
считаются известными.
На выходе звена (системы) следует ожидать также гармонический сигнал, но отличающийся от входного амплитудой и фазовым сдвигом.
В общем виде выходной сигнал:
![]()
где![]() – амплитуда выходного
гармонического сигнала, а
– амплитуда выходного
гармонического сигнала, а ![]() – фазовый сдвиг.
– фазовый сдвиг.
Из определения передаточной функции можно записать комплексную передаточную функцию разомкнутой ИС
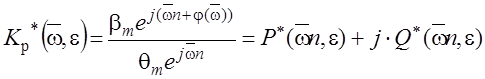
По отношению амплитуды ![]() и
и ![]() можно записать модуль
можно записать модуль
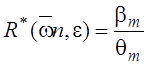
Тогда комплексная передаточная функция может быть записана
![]()
где
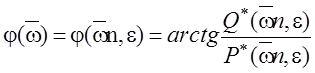 – ФЧХ
– ФЧХ
![]() – АЧХ
– АЧХ
В общем виде передаточную функцию разомкнутой ИС можно записать в виде
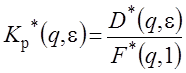
где ![]() полином числителя в степени m,
полином числителя в степени m, ![]() полином знаменателя степени n. Выражение
полином знаменателя степени n. Выражение ![]() является
дробно-рациональным, т.е. m≤n
запишем в общем виде передаточную функцию
является
дробно-рациональным, т.е. m≤n
запишем в общем виде передаточную функцию
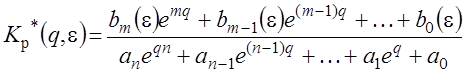 .
.
После подставки ![]() получаем комплексную
передаточную функцию разомкнутой ИС:
получаем комплексную
передаточную функцию разомкнутой ИС:
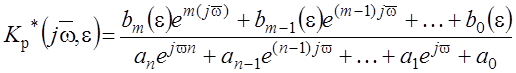 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.