Лекция 23.СТРУКТУРЫ УПРАВЛЕНИЯ
План
1.Структуры управления.
2. Реализация ПИД-регулятора.
3. Дискретная модель ПИД-регулятора.
4. Позиционный алгоритм ПИД-регулятора.
5. Алгоритм приращений.
6. Определение частоты выборки в СУ.
Цифровые технологии позволяют реализовать как дискретные, так и аналоговые регуляторы, а также нелинейные и самонастраивающиеся регуляторы. Главная проблема цифрового управления – найти соответствующую структуру регулятора и его параметры. Программная реализация алгоритмов управления по этим параметрам обычно является сравнительно простой задачей.
Каждый регулятор должен включать и средства защиты, предотвращающие опасное развитие процесса под действием регулятора в нештатных ситуациях.
Многие ТП характеризуются несколькими входными и выходными параметрами. Часто внутренние связи и взаимодействие соответствующих сигналов не имеют принципиального значения, и процессом можно управлять с помощью набора простых регуляторов, при этом каждый контур используется в системах прямого цифрового управления.
Линейные регуляторы с одним входом/выходом можно представить в обобщенном виде
|
|
(23.1) |
где u – это выход регулятора (управляющая переменная), uс – заданное значение, а у – выходной сигнал процесса (управляемая переменная). Параметр п представляет собой порядок регулятора.
Обычный ПИД-регулятор может рассматриваться как частный случай обобщенного дискретного регулятора при п = 2.
Рассмотрим регулятор, состоящий из двух частей: контура обратной связи (feedback) GFB(s), отрабатывающего ошибку E, и контура упреждения (feedforward) GFF(s), контролирующего изменения задающего воздействия и прибавляющего к управляющему сигналу поправочный член, с тем чтобы система реагировала более оперативно на изменения задания.
Для этого регулятора управляющее воздействие U(s) представляет собой сумму двух сигналов
|
|
Это выражение можно переписать в виде
|
|
(23.2) |
где UF1(s) – упреждающий сигнал по опорному значению (задающему воздействию), a UF2(s) – сигнал обратной связи.
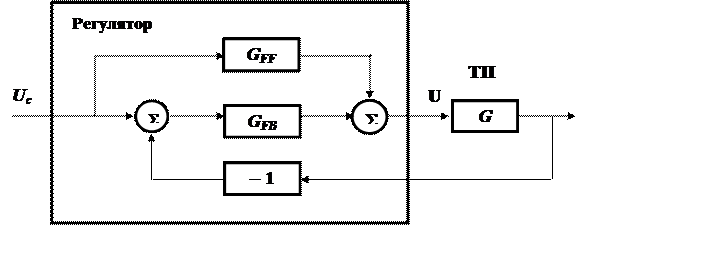 |
Рис.23.1. Регулятор,
содержащий контур упреждающего управления
по опорному значению (заданию) и контур обратной связи по выходу процесса
Регулятор имеет два входных сигнала Uc(s) и Y(s) и, следовательно, может быть описан двумя передаточными функциями GF1(s) и GR(s).
|
|
(23.3) |
Поскольку регулятор с ПФ (23.3) имеет за счет GF1(s) больше настраиваемых коэффициентов, чем обычный регулятор, то замкнутая СУ имеет лучшие характеристики.
Положение полюсов системы с обратной связью можно изменить с помощью регулятора GR(s), а упреждающий регулятор GF1(s) добавляет системе новые нули. Потому СУ может быстро реагировать на изменения сигнала задания, если GF1(s) выбрана правильно.
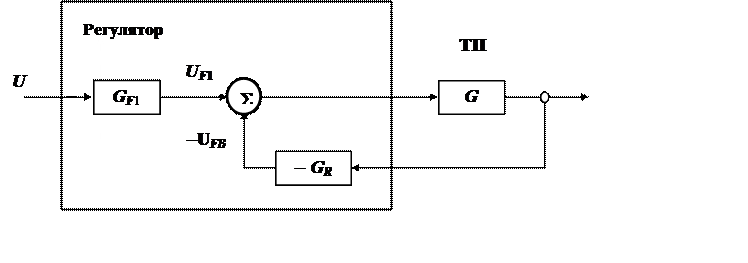 |
Рис.23.2. Структура линейного регулятора с упреждающим
управлением
и обратной связью
Благодаря использованию такого регулятора, возможно создание высокоточных (серво) СУ электроприводами, роботами или станками. Для них важно, чтобы реакция на выходную величину процесса была быстрой и точной при любых изменениях задания.
Если числитель и знаменатель ПФ GR(s), и GF1(s) в (23.3) выразить полиномами от s, то описание регулятора после преобразований можно представить в следующем виде
|
|
(23.4) |
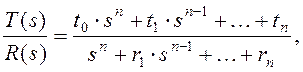 |
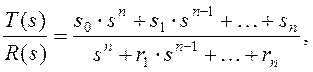 |
ri , si, ti –параметры полиномов ПФ, s – оператор Лапласа.
ПФ процесса можно выразить так
|
|
(23.5) |
Используя выражения (23.4) для регулятора и (23.5) для процесса, ПФ замкнутой системы можно записать так
|
|
(23.6) |
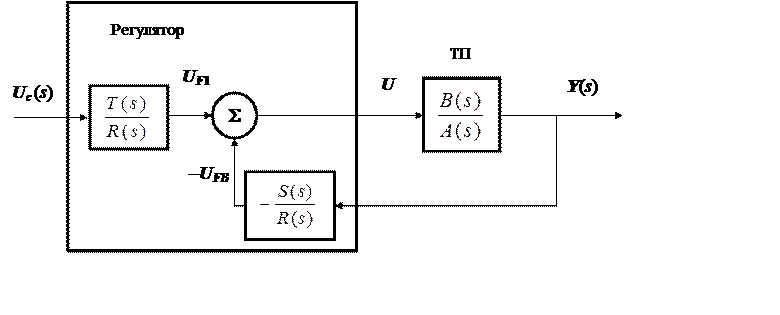
Рис.23.3. Структура линейного регулятора с упреждающим
управлением
и обратной связью в виде ПФ
Если R(s), S(s) и T(s) имеют достаточно высокий порядок, т. е. достаточное количество "ручек настройки", ПФ замкнутой системы можно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.