causal) фильтр вычисляет выходное значение на основании ранее введенных данных (в любой момент t0 учитываются входные значения только для t< t0). Поэтому все фильтры реального времени (on-line) являются причинными.
Последовательность отфильтрованных значений на выходе будет отставать на некоторое время по сравнению с последовательностью на входе.
Если данные обрабатываются в автономном режиме (off-line), например, при анализе серии значений уже собранных измерений, можно использовать непричинный (non-causal) фильтр.
В этом случае расчет для момента времени t0 можно производить на основе как предыдущих (t< t0), так и последующих (t> t0) значений.
Цифровые фильтры НЧ
Для анализа медленно изменяющегося входного сигнала из измерительных данных удаляют случайные пики и высокочастотные наводки с помощью ЦФ низкой частоты (digital low pass filter).
Как и у аналоговых фильтров ЦФ высокого порядка более эффективны для удаления нежелательных высоких частот.
ЦФ НЧ, используемые в промышленности, почти всегда базируются на фильтре скользящего среднего либо на фильтре экспоненциального сглаживания (exponential smoothing).
Фильтр скользящего среднего
Это простейший ФНЧ. Он получается, если принять в уравнении (25.1) все параметры аi равными нулю. Если необходимо простое усреднение, то все весовые коэффициенты bi равны и дают в сумме единицу.
Так, фильтр скользящего среднего с пятью входными отсчетами имеет вид
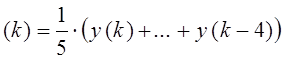 .
.
Если фильтрация проходит не в режиме реального времени, то величину скользящего среднего можно подсчитать, используя измерения как до, так и после заданного момента времени k= kts.
В этом случае отфильтрованное значение не отстает по времени относительно входных значений. Непричинный простой фильтр скользящего среднего по пяти значениям имеет вид
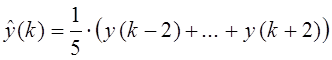 .
.
Если выход ЦФ является усреднением по последним п выборкам, то она смещается на 1 + п /2 циклов. При больших п выходной сигнал становится более гладким, но при этом все больше отстает по времени. Импульсная характеристика ЦФ скользящего среднего конечна.
Для входного импульса в момент t = 0 выходной сигнал после момента t = п становится нулевым.
Скользящее среднее – это простой метод, но он имеет ограничения.
При использовании одинаковых коэффициентов фильтр излишне инертен и недостаточно быстро реагирует на реальные изменения во входном сигнале.
С другой стороны, если коэффициенты различны и убывают для больших значений индекса п, то это затрудняет анализ свойств фильтра.
Экспоненциальный фильтр
Это авторегрессионный фильтр (exponential filter) скользящего среднего первого порядка, определяемый следующим уравнением
|
|
(25.2) |
Весовой коэффициент α лежит в интервале между 0 и 1. Уравнение (25.2) можно переписать в виде
![]() ,
,
т.е. экспоненциальный фильтр уточняет отфильтрованное значение на выходе сразу, как только на вход поступает новое значение.
Это уточнение невелико, особенно при α, близких к 1. Уменьшение шумовых компонентов выходного сигнала происходит за счет слабого соответствия с реальными изменениями на входе.
При α, близком к нулю, величина поправки растет. При этом фильтрация шума уменьшится, однако изменения исходного сигнала будут отслеживаться более точно. При α = 0 сигнал на выходе идентичен сигналу на входе.
Влияние величины α на реакцию фильтра при скачке зашумленного входного сигнала показано на рис. 25.1.
При больших a фильтр вносит запаздывание, но зато шумы меньше.
Экспоненциальный фильтр можно представить как фильтр скользящего
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.