Расчет системы автоматического регулирования скорости вращения вала двигателя постоянного тока с независимым возбуждением, страница 3

Передаточная функция замкнутой системы с учетом отрицательной единичной обратной связи:

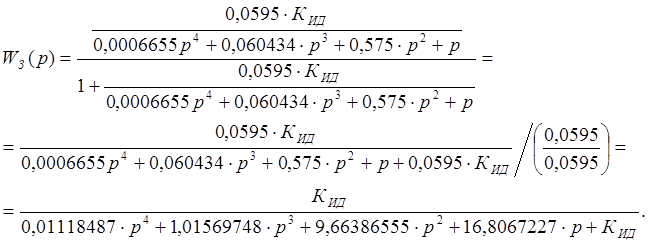
Характеристическое уравнение имеет вид:

.

Для определения устойчивости замкнутой системы воспользуемся критерием Гурвица.

Составим главный определитель Гурвица на порядок ниже, чем порядок уравнения, т.е. третьего порядка.

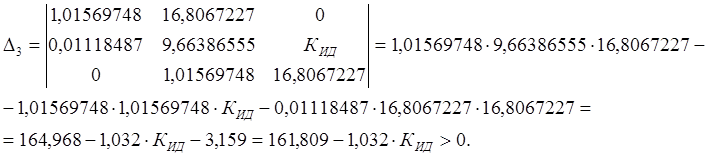
Выбираем К_ИД, с условием, что К_ИД<156,792, он равен К_ИД=0,4×156,792=62,72,  главный определитель Гурвица будет больше нуля.

Критический коэффициент усиления: К_кр=156,792.

Составляем диагональные миноры определителя Гурвица:

,

.

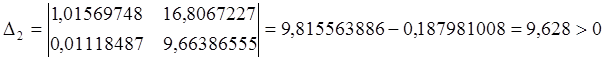Диагональные миноры также больше нуля.

Согласно определению критерия Гурвица наша система в замкнутом состоянии является устойчивой, т.к. главный определитель Гурвица и все его диагональные миноры больше нуля.

4 Построение переходного процесса по вещественной частотной характеристике замкнутой системы

Получим вещественную частотную характеристику Р_З(w) АСР путем подстановки в передаточную функцию замкнутой системы выражения р=jw и отделением вещественной части:

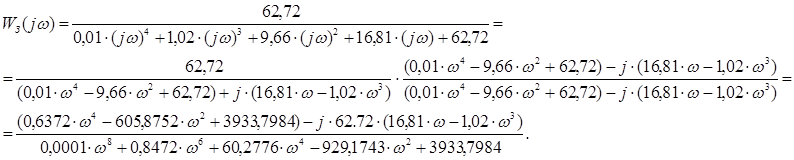
Выделяем вещественную часть выражения и получаем уравнение вещественной частотной характеристики:

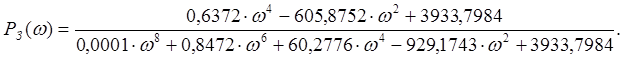
Изменяя значения w от 0 до ¥, строим вещественную частотную характеристику. ВЧХ представлена на рисунке 3.

Таблица 4                           Данные для построения ВЧХ

w	0	0,5	1	1,5	2	2,5
P(w)	1	1.02080	1.08572	1.19267	1.23025	0.249363

Продолжение таблицы 4

w	3	3,5	4	4,5	5	5,5
P(w)	-1.36969	-1.07527	-0.702171	-0.478345	-0.341849	-0.253490

Окончание таблицы 4

w	6	6,5	7	7,5	8	8,5
P(w)	-0.193263	-0.150523	-0.119226	-0.095733	-0.077742	-0.063738

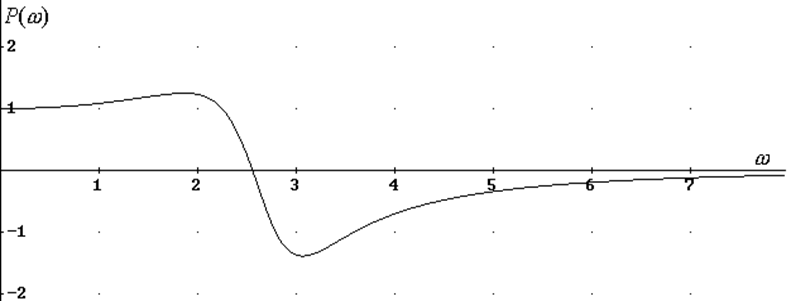
Рисунок 3 Вещественная частотная характеристика

Полученную ВЧХ разбиваем на трапеции (рисунок 4). Для каждой трапеции определяем параметры, которые сводим в таблицу 5.

Таблица 5                           Параметры трапеций

	Трапеция1	Трапеция2	Трапеция3	Трапеция4
ri	0,25	2,6	0,9	0,45
wd	0,56	2,2	3,15	4,26
wc	2,0	2,89	4,26	7,25
	0,3	0,76	0,74	0,59

Для проверки правильности разбивки ВЧХ воспользуемся формулой:

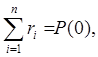
где r_i - высота i-ой трапеции; Р(0) – значение Р(w) при w=0.

Согласно разбивки на трапеции следует что:

                                         Р_З(w)= -ТрI+ТрII-ТрIII-ТрIV                            (4)

Воспользовавшись формулой (4) имеем:

-0,25+2,6-0,9-0,45=1, что соответствует действительности.

Для каждой трапеции выпишем в отдельные таблицы значения h-функций при соответствующих À. При заполнении таблиц воспользуемся следующими формулами: 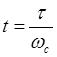 - реальное время, с;  - реальное значение h-функции

Таблица 6                              Данные трапеции I

À=0,3

t	1	0	1	2	3	4	5	6	7	8	9	10
h(t)	2	0	0,401	0,681	0,958	1,06	1,087	1,065	1,037	1,021	1,018	1,019
t	3	0	0,5	1	1,5	2	2,5	3	3,5	4	4,5	5
h(t)	4	0	0,100	0,170	0,230	0,265	0,272	0,266	0,259	0,255	0,255	0,255

Окончание таблицы 6