Определение качества обработки поверхностей с помощью микроинтерферометра, страница 2

          Пусть две волны одинаковой частоты, накладываясь друг на друга, возбуждают в некоторой точке колебания одинакового направления

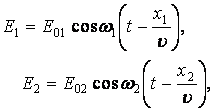
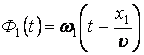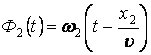где Е₀₁, Е₀₂ – амплитудные значения светового вектора, а величины  и  представляют собой фазы колебаний.

          Результирующее колебание в общем случае определяется в соответствии с принципом суперпозиции. В нашем случае (колебания одинакового направления) удобно воспользоваться графическим методом векторного сложения амплитуд. Под вектором амплитуды понимается вектор , модуль которого равен значению амплитуды, а угол который этот вектор  составляет с заданной осью х соответствует фазе колебания  (см. рис.1)

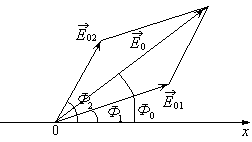
Рис. 1.

          Обратите внимание, проекция вектора Е₁ и соответственно Е₂ на ось х представляют собой складываемые состояния колебаний в данный момент времени, вектор  представляет собой вектор амплитуды результирующего колебания, а угол  – фазу результирующего колебания. С изменением времени  вектора ,  и  будут вращаться вокруг оси, при этом форма параллелограмма и угол  будут меняться сложным образом, так что результирующее колебание не будет гармоническим. Амплитуда этого колебания определяется уравнением:

,

а фаза

.

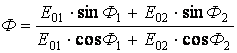Как известно, интенсивность волны (в данном случае освещенность) пропорциональна квадрату амплитуды колебания, а в нашем случае

.

          Таким образом, интенсивность светового поля будет пульсировать между крайними значениями с частотой ~10¹⁵ с^-1. Но ни глаз и ни один оптический прибор не в состоянии фиксировать мгновенное состояние светового поля, измеряющегося с такой огромной частотой, а способно лишь фиксировать его среднее значение:

.

          Вот откуда и следует известный закон фотометрии: освещенность от двух источников равна сумме освещенностей.

          Представляет интерес частный случай, когда  и разность фаз  не зависит от времени и остается постоянной. Волны, удовлетворяющие этим условиям называются когерентными. В световом поле когерентных источников света происходит стационарное (не зависящее от времени) перераспределение энергии, в результате которого в одних местах происходит усиление интенсивности (максимум интерференции), а в других ослабление интенсивности (минимум интенсивности). Условия максимума и минимума интерференции получаются из очевидных соображений

;

.

Числа k и т называют соответственно порядком максимума и порядком минимума.

          С учетом того, что  условия максимума и минимума можно записать так