Многомерные СУ, их математическое описание. Метод пространства состояния. Собственные значения и вектора матрицы

Лекция 2.

1. Многомерные СУ,  их математическое описание.

2. Метод пространства состояния.

3. Определения обратной матрицы.

4. Собственные значения и вектора матрицы.

5. Способ описания “вход-выход”.

Многомерные СУ

СУ сложными ТП часто содержат элементы с несколькими входными и выходными переменными. Такие элементы называют многомерными.

Многомерными элементами (МЭ) являются и ОУ. Так, электрический  генератор a.c. имеет две выходные переменные – напряжение и частоту и две входные – напряжение возбуждения и частоту вращения ротора.

Для ТП флотации медной руды к выходным переменным относятся показатели качества медного концентрата (содержания меди и посторонних компонентов) и большое количество режимных параметров (плотность пульпы, размеры минеральных частиц и т. д.).

К входным управляемым переменным относятся подача реагентов, уровни пульпы в флотокамерах.

МЭ могут быть и многоканальные регуляторы в виде микропроцессорных контроллеров. В качестве выходных величин могут использоваться абстрактные переменные (производные), не имеющие конкретного физического смысла.

Тогда и одномерный элемент (но выше первого порядка) может рассматриваться как многомерный.

Для математического описания МЭ используют:

 Ä  динамические характеристики (диф. уравнения, ПФ,  частотные характеристики) для реальных входных и выходных переменных  –  метод “вход-выход” или Input/Output – IO;

 Ä диф. уравнения в форме Коши для абстрактных выходных – переменных состояния – метод пространства состояния (ПС) или State Space – SS.

Метод пространства состояния

Понятие состояния, лежащее в основе современного подхода к описанию динамических систем, было введено Тьюрингом в 1936 г. Позднее метод  ПС для анализа и синтеза оптимальных СУ использовал Беллман, затем  Калман, оказавший своими работами значительное влияние на современное состояние ТАУ.

С точки зрения анализа и синтеза СУ целесообразно разделить все переменные, характеризующие систему или имеющие к ней определенное отношение, на три группы, а именно:

 1) входные переменные или воздействия ui - сигналы, генерируемые системами, внешними по отношению к исследуемой системе;

2) выходные переменные или переменные, характеризующие реакцию системы yj;

  3) переменные (координаты) состояния или промежуточные переменные xk, характеризующие динамическое поведение исследуемой системы.

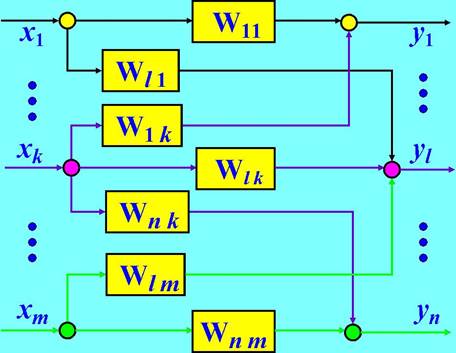
Схематически система может быть изображена в виде “черного ящика” с некоторым числом входных и выходных каналов.

Входные каналы  – это совокупность входных переменных или входных воздействий ui; выходные каналы  – совокупность выходных переменных или выходных координат yj системы.

Промежуточные переменные  – координаты состояния xkотнесены к содержимому “черного ящика” и скрыты от наблюдателя.   Величины ui, yj и xkявляются функциями времени ui(t), yj(t) и xk(t) для момента  t.

Для удобства оперирования с многомерными величинами совокупность входных переменных представляют в виде вектора входа

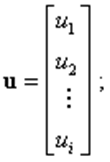
совокупности выходных переменных  и переменных состояния  –  в виде, соответственно, вектора выхода и вектора состояния

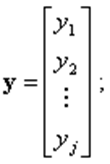
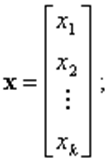
Согласно понятию векторного пространства множество всех значений, которые может принять вектор входа u в момент t, образует пространство входа системы.  Множество всех значений, которые может принять вектор выхода у в момент t, образует пространство выхода системы, и множество всех значений, которые может принять вектор состояния х,  - пространство состояний системы.

В любой момент t состояние системы есть функция начального состояния x(t0) и  вектора входа u (t0, t), т. е.

x(t) = F[x(t0); u(t0, t)],                                                   (3.1)

где F  -  однозначная функция своих аргументов.

Вектор выхода в момент t является также функцией x(t0) и u(t0, t) и может быть записан как

y(t) = j[x(t0); u(t0, t)].                                                  (3.2)

Уравнения (3.1) и (3.2) называются уравнениями состояния системы.