Для систем, описываемых диф. уравнениями в форме Коши, уравнения (3.1) и (3.2) могут быть записаны в общей форме:
![]()
![]()
где ![]() -
вектор первых производных переменных состояния.
-
вектор первых производных переменных состояния.
![]()
![]()
Если система описывается линейными диф. уравнениями, то уравнения состояния системы таковы:
![]()
![]()
где A (t) – матрица коэффициентов;
В (t) – матрица управления;
C (t) – матрица выхода;
D (t) – матрица обхода системы.
С учетом векторов возмущений на входе w(t) и выходе v(t) системы уравнения состояния будут иметь вид:
![]()
![]()
Если элементы матриц A, В, C и D не зависят от времени, а возмущений w(t) и v(t) нет, то
![]()
![]()
В области изображений уравнения состояния имеют вид:
![]()
![]() (3.3)
(3.3)
Откуда
![]()
или
![]()
гдеI- единичная
матрица.
С учетом этого уравнение выхода имеет вид
![]()
или
![]() (3.4)
(3.4)
гдеW(s) - матричная ПФ системы.
Порядок определения матрицы, обратной для [Is -A].
1. Составляют матрицу, каждый элемент которой - алгебраическое дополнение соответствующего элемента [Is -A], т.е. минор этого элемента, умноженный на (-1)i + j.
Минор элемента - это детерминант матрицы, полученной вычеркиванием i-строки иj-го столбца.
2. Транспонированием полученной матрицы находят присоединенную для [Is -A] матрицу adj [Is -A].
3. Вычисляют определитель ½Is -A½.
4. Определяют обратную для [Is -A] матрицу по формуле:
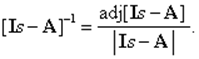 (3.5)
(3.5)
Матрица Ф(t), определяемая обратным преобразованием Лапласа,
![]() (3.6)
(3.6)
называется переходной (фундаментальной) матрицей. Она также может быть найдена из выражения
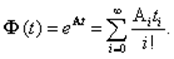 (3.7)
(3.7)
Изменение вектора состояния во времени при известном векторе управления определяется решением уравнения
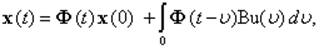 (3.8)
(3.8)
где х(0) - начальное положение вектора х(t) в момент t = 0.
При расчете СУ часто необходимо найти значения l, для которых существуют решения системы однородных алгебраических уравнений
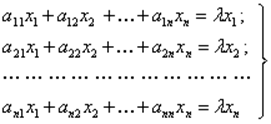 (3.9)
(3.9)
Значения
l называются собственными значениями матрицы А = [aij].
Соответствующие им векторные решения собственными векторами матрицы А.
В векторных обозначениях система уравнений (3.9) имеет вид
А x = lx.
Откуда
[А - lI] = 0. (3.10)
Уравнение (3.10) имеет решение только, когда определитель ½А - lI½ равен нулю, т.е.
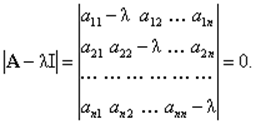 (3.11)
(3.11)
Разложение определителя приводит к характеристическому уравнению, из которого находятся все nсобственных значений l1, l2, …, ln, матрицы А.
Определитель ½А - l I½можно записать в виде полинома n-й степени
f(l) =½А - l I½= (- l)n + bn-1 (- l) n-1 + …+ b1 (- l) + b0 . Функция f(l) называется характеристической или собственной функцией матрицы А .
Способ описания “вход-выход”
При его использовании для описания многомерных систем применяют выражение с ПФ (3.4):
![]()
где
![]() (3.12)
(3.12)
Матрицы с элементами в виде весовых wij(t)или переходных hij(t)
функций называются соответственно весовой
w(t)или переходной h(t)
матрицами. Передаточная и весовая матрицы связаны соотношением
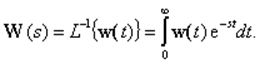
Если воздействия приложены к элементу одновременно в момент t= 0, то
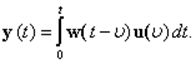
или в скалярной форме
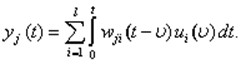
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.