Методы параметрической идентификации. Методы структурной идентификации объектов управления. Методы планирования эксперимента (полный факторный эксперимент). Аналитический метод построения математических моделей, страница 3

y_i – модель,полученная в ходе эксперимента

Метод наименьших квадратов.

Исп-ся для определения коэф-в Ур-я регрессии. Алгоритм:

1. Выберем линейную модель

2. Полученная модель должна иметь минимальную ошибку, кот.опр-ся по критерию оптимальности:

3.Исходные экспериментальные данные.

Для опр-я коэф-в а0, а1, а2, и т.д.возьмем частные производные от критерия по всем параметрам. Получим сист. У-й:

4. В результате получим следующие коэффициенты:

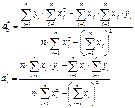Проводится несколько экспериментов.

5. Для проверки гипотезы линейной связи между y и x вычисляется коэффициент корреляции R:

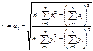где r = 0…1.

Коэф-т корреляции показывает степент тесноты м-у пар-ми. Если R = 0, то связь отсутствует. Если r > 0.7 , то гипотеза о линейности верна,

если r < 0.3 , то гипотеза не верна. В тех случаях когда лин-я модель не пригодна, нужно переходить к более сложным моделям, не рекомендуется исп-ть полиномы в степени выше 3.

Если нет, то модель(ее структура) пересматривается в сторону усложнения. Исходные денные для получения коэффициента регрессии могут быть получены 2-мя путями:

а)В рез-те пассивного наблюдения за процессом.

в)Путем подстановки активного(заранее спланированного) эксперимента.

Опытные данные получают при пассивном эксперименте-выбрать наиболее сущесвенные факторы. Оценить интервал наблюдения и т.д. Характерная особенность: отсутствие вмешательства в технологический процесс, что имеет ряд преимуществ, как с точки зрения простоты реализации, так и возможности исключения аварийной ситуации.

Недостатки пассивного экперимента:

1) Входные величины х1,х2,…,хк должны измеряться с точностью значительно превышающей точность выходной величины у.

2) Выходные величины должны быть стохастически независимы.

3) Выходной параметр у-есть случайная величина, которая должна подчиняться закону нормального распределения.

4) Дисперсия выходного параметра у должна быть постоянна.

5) Очень сложно решается задача введения в уравнение регрессии новых данных(переменных) и отбраковка.

6) При вычислении коэффициента ур-ий регрессии некоторые из них оказываются незначительными, хотя при определенных условиях они оказывают существенное влияние на выходную величину у.

4.Методы планирования эксперимента (полный факторный эксперимент)

1)АКТИВНЫЙ МЕТОД-ПОЛНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТ.

Активный эксперимент устраняет все недостатки пассивного эксперимента. Он основан на активном вмешательстве в технологический процесс(в его нормальный режим). Идея метода состоит в варьировании всеми переменными по определенному плану, что позволяет существенно сократить кол-во опытов.

1-й этап. Нормирование входных параметров(переменных).

Для определения ур-ия регрессии данного вида(линейного) входные переменные (варьируемые факторы) поддерживаются на заранее выбранных фиксированных уровнях. Этих уровней обычно n=2, 3.

N=2 x_imax=1 x_imin=0

N=3 x_imax=1 x_iср=0 x_imin=-1 (1,0,-1 – кодированные величины)

x_i₀ – среднее значение. x_i₀=