Методы параметрической идентификации объектов управления. Методы математической обработки экспериментальной информации (регрессионный анализ). Аналитический метод построения математических моделей на основе мгновенных балансов потоков веществ и энергии, страница 3

y=a0+a1x1+a2x2…

2. Определяем коэффициенты а1, а2, а3...

3. Определяем критерий оптимальности (точности)

4. Определяем оптимальные значения коэффициентов.

Метод наименьших квадратов для определения а1, а2, а3...

1. Выбираем мат. модель вида:

2. Определяем критерий точности.

3. Берем частные производные от критерия точности по всем параметрам.

4. Решаем совместно уравнение, составленное в первом и третьем пункте, и находим коэффициенты а1, а2, а3 и.т.д.

В результате проведен эксперимент, в результате которого получено какое-то число опытов, изображаем графически результат этих опытов, для проверки адекватности модели и определения связи между параметрами вычисляем коэффициент корреляции, который показывает степень тесноты линейной связи между Х и У. Если он = от 0,7 до 1 модель адекватна.

Линейный множественный регрессионный анализ.

Задача: построить такое уравнение плоскости, отклонения результатов наблюдейний от которого были бы минимальны.

Проводят эксперименты, записывают показания приборов о состоянии выходной величины У и всех факторов, от которых она зависит Х, и в получаем матрицу

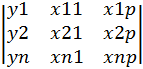
n – количество опытов, р – число факторов, х21 – значение фактора 1 для 2 опыта.

Уравнение:

Находим коэффициенты а1, а2 и т.д. затем записывают окончательное уравнение регрессии.

Нелинейный множественный регрессионный анализ.

Используют:

1) полиноминальную модель – здесь не рекомендуется использовать полином в степени выше 3, хотя использование полиномов высоких степеней дают результаты, хорошо согласующиеся с экспериментальными данными. Форма кривой может ввести в заблуждение, т.к. полиномы высоких степеней имеют тенденцию описывать колебания кривой, т.е. давать частые провалы и выбросы.

2)мультипликативная модель

3)экспоненциальная модель – линеаризуют уравнение регрессии, потом выполняют все операции линейного множественного регрессионного анализа.

4 Методы планирования эксперимента (полный факторный эксперимент).

Бывают:

1) полный факторный эксперимент (ПФЭ)

2) дробный факторный эксперимент (ДФЭ)

При планировании ПФЭ реализуются все возможные комбинации факторов на всех выбранных для исследования уровнях.

Объект управления:

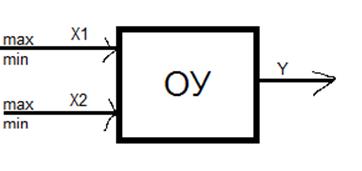
min и max – уровни

Количество опытов определяются по формуле: N=n^k, n – число уровней, к – число факторов.

Для составления плана эксперимента кодируют число уровней:

Xmax=+1

Xmin=-1

Xср=0

Средний нулевой уровень, около которого варьируем:

Шаг варьирования:

При таком расположении опытов матрицы благодаря переходу к кодированным переменным автоматически выполняется условие статической независимости варьируемых факторов(условие ортогональности).

Переход от натуральных к кодированным переменным:

Схема проведения эксперимента изображается в виде матрицы. Матрица планирования эксперимента изображается по принципу ни одной повторяющейся комбинации уровней и факторов.

Недостаток ПФЭ: при введении каждого нового фактора число опытов удваивается.

Идея: реализуется не вся матрица ПФЭ, а только ее часть.

Для сокращения числа опытов используют дробный факторный эксперимент (ДФЭ), который заключается в том, что реализуется не вся матрица ПФЭ, а, например, четвертая или восьмая ее часть.

Алгоритм планирования эксперимента в общем виде:

1. Выбираются факторы Х1, Х2, Х3 и т.д. и функция отклика У.

2. Определяется число уровней.

3. Составляется матрица планирования эксперимента (ПФЭ или ДФЭ)

4. Постановка опытов с учетом знаков факторов. Опыты проводят в случайном порядке, чтобы устранить систематические ошибки.