Автоматизация технологических процессов и производств: Методические указания к практическим занятиям

График возмущающего воздействия X(t) и кривая разгона объекта – изменение уровня воды ∆H(t) представлен на рисунке 1.4.

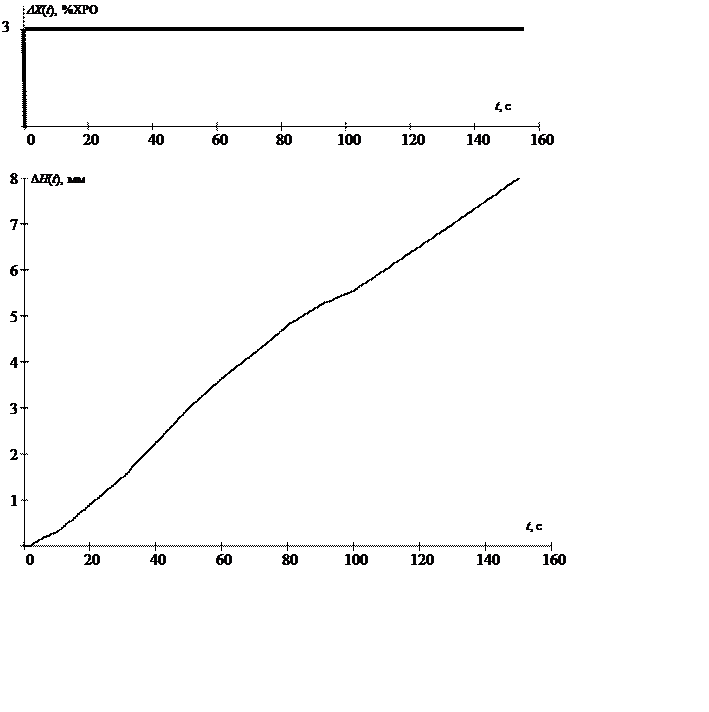
Рисунок 1.4 – График возмущающего воздействия и кривая разгона объекта

Единичная DH⁰(t)  переходная функция определяется по следующей формуле:

DH⁰(t) = DH(t) / A,                                                                        

где A – скачкообразное возмущающее воздействие, при котором снята переходная характеристика (А = 3 % ХРО).

Результаты расчётов единичной  переходной функции сведены в таблицу 1.5.

Таблица 1.5 – Ординаты единичной переходной функций

Окончание таблицы 1.5

На рисунке 1.5 приведена единичная переходная характеристика.

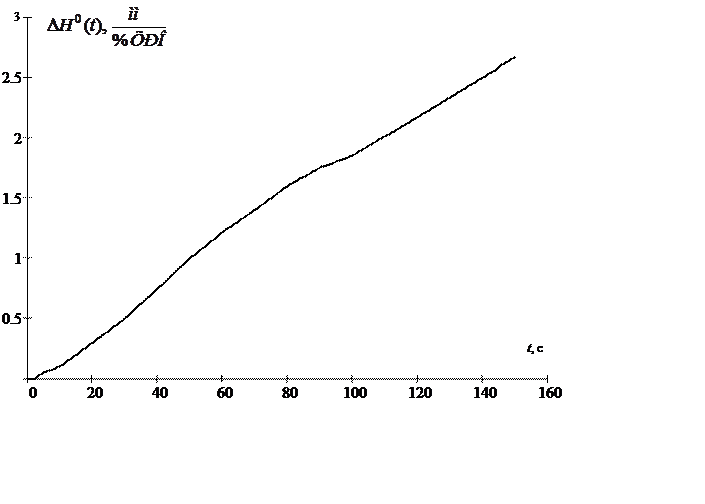
Рисунок 1.5 – Единичная переходная характеристика

При аппроксимации объекта последовательным соединением астатического звена и звена запаздывания его передаточная функция будет иметь вид [1.2, с. 90-93; 1.3, с. 226-239]:

.

Динамические характеристики объекта:

- запаздывание объекта определяется как отрезок времени (0; t), на котором выполняется равенство DH⁰(t) =0; по графику на рисунке 1.5 и таблице 1.5 определяем t = 2 с;

- коэффициент передачи объекта определяется как тангенс угла наклона прямой, соответствующей средней скорости изменения уровня, т.е. K_об = 0,0188 .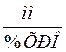

Таким образом, аппроксимирующая передаточная функция примет вид:

.

Для оценки точности аппроксимации экспериментальной переходной функции решением дифференциального уравнения первого порядка с запаздывающим аргументом рассчитываются ординаты аппроксимирующей кривой:

Далее вычисляются разности d_ап:

и ошибки между ординатами переходных функций δi:

Результаты расчётов сведены в таблицу 1.6.

Таблица 1.6 – Ординаты переходных функций

t, с	0	2	10	20	30	40	50	60	70	80	90
,мм	0,00	0,00	0,11	0,32	0,50	0,75	0,93	1,12	1,30	1,50	1,67
,мм	0,00	0,00	0,15	0,34	0,53	0,71	0,90	1,10	1,28	1,47	1,65
dап×102	0,00	0,00	0,16	0,04	0,09	0,16	0,09	0,04	0,04	0,09	0,04
δi,%	0	0	12,1	3,5	4,2	4,6	3,1	1,9	1,8	2,5	1,6

Окончание таблицы 1.6.

t, с	100	130	150
,мм	1,88	2,43	2,78
,мм	1,84	2,41	2,78
dап×102	0,16	0,04	0
δi,%	2,9	1,3	0

Используя данные таблицы 1.6 строим исходную и аппроксимирующую единичные переходные функции (рисунок 1.6) и визуально оцениваем степень их близости.

Далее вычисляем среднюю ошибку аппроксимации δ_ср:

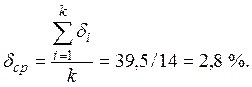
Так как средняя ошибка  аппроксимации менее 3% считаем найденное математическое описание котла по каналу: изменение подачи воды - уровень воды в барабане приемлемым.

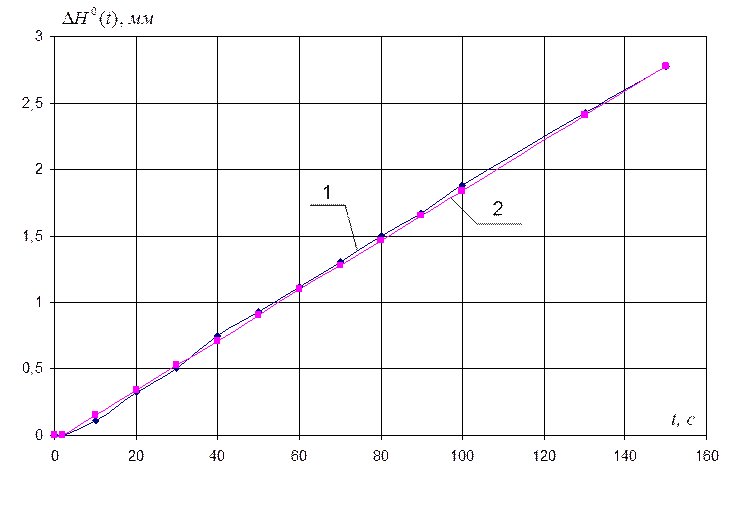
Рисунок 1.6 – Единичные переходные характеристики: 1 – исходная;

2 – аппроксимирующая

1.3. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Под математическим описанием объекта регулирования понимается совокупность уравнений статики и динамики. Первые описывают, характер связей между входными и выходными координатами объекта в установившемся режиме работы и в подавляющем большинстве случаев являются алгебраическими уравнениями типа

y=f(x₁, x₂,…, x_k),    k≤2÷5,

где у- выходная регулируемая координата (давление, концентрация, температура и т.д.), (x₁, x₂,…, x_k) - входные (воз­мущающие или регулирующие) координаты. Функция f чаще, всего нелинейна, однако не имеет разрывов первого и второго рода и может быть линеаризована в определенном интервале изменения x₁, x₂,…, x_k.

Уравнения динамики характеризуют поведение выходной координаты объекта y в переходном режиме работы, т.е. при изменении какой-либо из координат x₁, x₂,…, x_k. Динамика объекта описывается дифференциальными уравнениями в полных или частных производных (реже — интегральными уравнениями).

Составление математического описания технологического объекта является достаточно трудной задачей, однако без знания уравнений статики и динамики невозможно построение качественно работающей системы автоматического регулирования.

При составлении математического описания объекта управления определяются его статические (коэффициент усиления - K_об, а иногда и вид статической зависимости) и динамические (запаздывание - t, постоянные