Составление плана производства, максимизирующего прибыль фирмы за рассматриваемый период

Задание 1. Фирма применяет n однопродуктовых технологий, которые используют m ресурсов. Технология jΠпри единичной интенсивности производит единицу продукта j и потребляет a_ij единиц ресурса i для каждого iÎ. В течение рассматриваемого периода фирма может использовать не более b_i единиц ресурса i. Известны рыночные цены продуктов и ресурсов: p_j для jΠи q_i для iÎ. Нужно найти план производства, максимизирующий прибыль фирмы за рассматриваемый период.

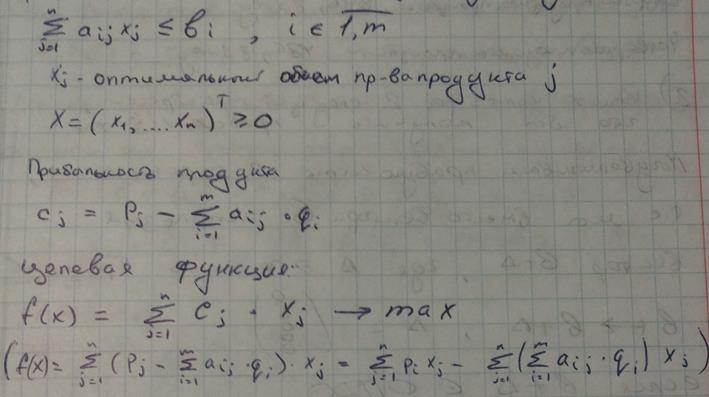(а) Запишите математическую модель задачи.

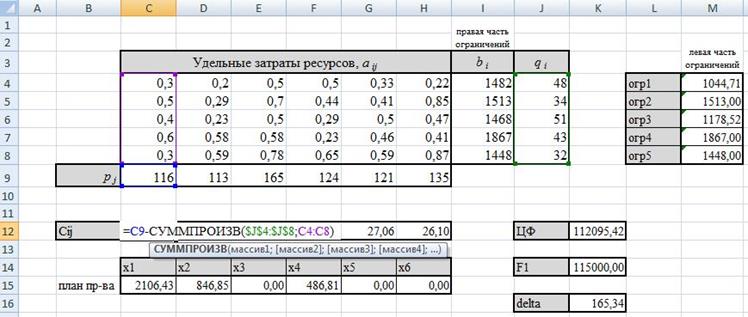
(б) Решите задачу при следующих исходных данных: m = 5, n = 6,

	Удельные затраты ресурсов, aij						bi	qi
	0,3	0,5	0,5	0,41	0,2	0,4	1886	49
	0,4	0,3	0,4	0,4	0,2	0,2	1108	51
	0,6	0,2	0,3	0,4	0,3	0,5	1955	46
	0,6	0,9	0,7	0,7	0,6	0,7	1600	28
	0,2	0,5	0,6	0,7	0,7	0,3	600	39
pj	123	134	144	143	106	130

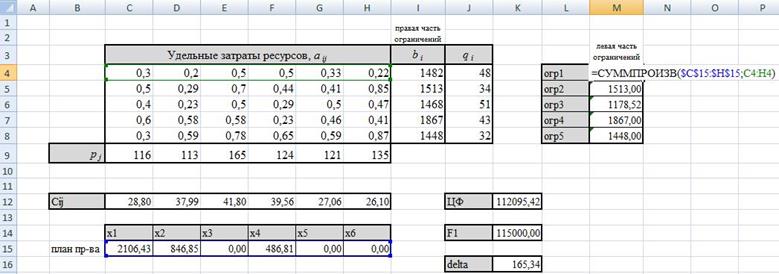
Поиск решения ЦФ =>  max

Изменяя план пр-ва

Ограничения: левые части ≤ правые части огр,

Параметры: линейная модель, неотриц значения

ЦФ=112 095,42

(в) Запишите оптимальный план производства.

В оптимальный план вошли продукт 1, 2, 4

Первого продукта произвести 2106,43 единиц

Второго продукта произвести 846,85единиц

Четвертого продукта произвести 486,81 единиц

(г) Какое дополнительное количество ресурса 2 следует приобрести (по той же цене), чтобы получить прибыль примерно 115 000?

Мы увеличиваем правую часть второго ограничения, т.е., мы вместо вектора b используя вектор b+D, где D=

Если b+D Î ОПДО (ОПДО – это множество таких векторов b, для которых базис  сохраняется, двойственные оценки не изменяются)

При этом множество d при котором вектор b+D Î ОПДО указано в отчете по устойчивости (Допустимое уменьшение, Допустимое увеличение)

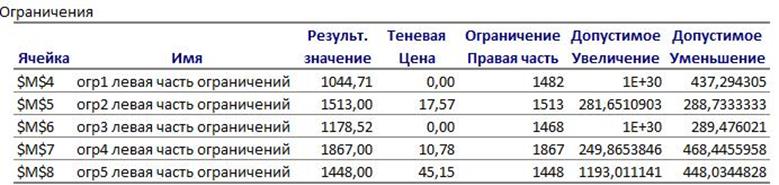
dÎ [-288,73; 281,65]

После расчета d необходимо проверить, что бы она попадала в эту область.

Если вектор правых частей измененных Î ОПДО, то

F(b) – оптимальное значение ЦФ

Прирост ЦФ – опт. знач. ЦФ = сумме произведения оценок на приросты правых частей:

F(b+D)-F(b)= Syi×di = y2 × d = 17,57× d= 115 000 – F

D2= 165,34

Поскольку D2 лежит в указанном диапазоне, то значение ЦФ при таком изменении будет равна примерно 115 000.

(д) Выгодно ли фирме продать некоторое количество ресурса 2 по цене 50?

Смотрим теневую цену: единица второго ресурса дает прибыль 17,57 пока вектор  правых частей остается в ОПДО каждая ед. второго ресурса дает такую прибыль. Продать ед. ресурса 2 значит потерять прибыль 17,57. Прибыль от продажи = разнице цен. Предлагается продать за 50, а цена ресурса 2 была 34

50-34=16,

А теневая цена 17,57 => не выгодно продавать. Т.к. потеряем больше, чем приобретем.

(е) На сколько процентов фирма может снизить цену продукта 4, сохраняя его оптимальный план?

Мы изменяем цену 4 продукта  => вектор с → с+D, где D есть вектор длины 6,

D = (0,0,0,d,0,0)

Если такое изменение не выводит вектор с из ОПОР, то оптимальный план менять не надо, он сохраняется. В каких границах должна меняться d указано в отчете по устойчивости.

С4=P4-Saij×qi = (10,419/124)×100% = 8,4%

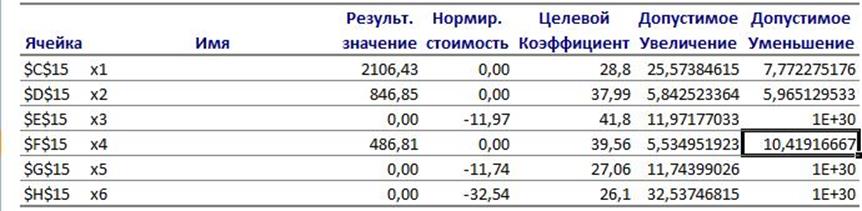На 8,4% процента фирма может снизить цену продукта 4, сохраняя его оптимальный план

Задание 2. Запишите задачу, двойственную к следующей задаче линейного программирования:

8x₁ -9x₂ + 3x₃ → max при условиях

6x₁ + 9x₂ - 4x₃ ≤ 16,  2x₁ - 7x₂ + 8x₃ = 12,  -9x₁ + 6x₂ + 2x₃ ≥ 20,  x₁ ≥ 0,   x₂ ≤ 0.

Задание 3. В таблице указаны участки железнодорожной сети (i, j) и затраты c_ij на транспортировку одного вагона между станциями i и j (независимо от направления). Стрелки в первой строке показывают возможные направления перевозок.

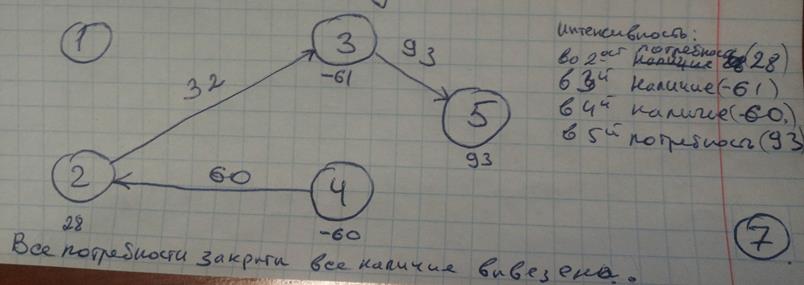
На станциях 3 и 4 находятся 61 вагон и 60 вагонов соответственно. Нужно отправить 93 вагона на станцию 5 и 28 вагонов на станцию 2.

(а) Запишите сетевые ограничения для вершин 1, 3 и 5.

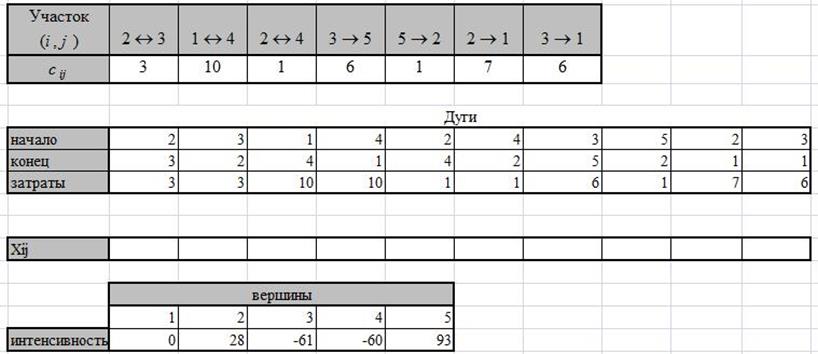
Положительная интенсивность означает потребность

Отрицательная интенсивность означает наличие.

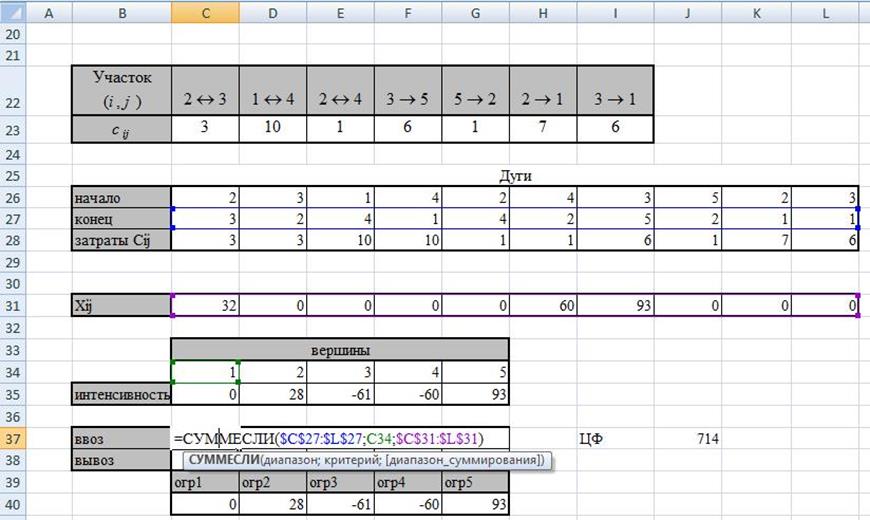
ввоз

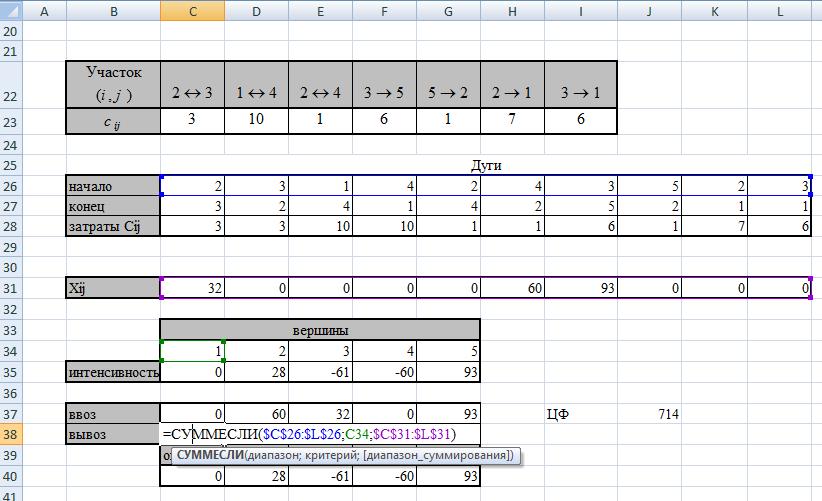 вывоз

ограничения: ввоз – вывоз.

Поиск решения.

ЦФ → min

Изменяя Хij

Ограничения: левые части ограничений (С40;G40) ≥ интенсивность (С35;G35)

32 везем по дуге X23

60 везем по дуге X42

93 везем по дуге X35

Затраты = 714

(б) Найдите минимальную стоимость перевозок и план, при котором она достигается.

Минимальную стоимость перевозок = 714

План:

X23 = 32

X42 = 60

X35 = 93

 (в) Нарисуйте схему оптимальных перевозок.

Задание 4. Дана матричная игра G = (A):

-5	1	4
1	-1	0
-6	-8	5
-4	5	-3

(строки соответствуют стратегиям игрока 1, столбцы — стратегиям игрока 2).

(а) Найдите максиминную чистую стратегию игрока 1 и минимаксную чистую стратегию игрока 2. Существует ли равновесие?

Анализируем игру в чистых стратегиях.

Для первого игрока:

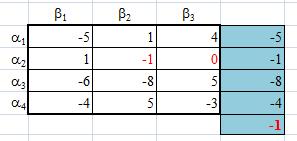Он выбирает минимум по строке, т.е. худший результат при каждой своей стратегии, и среди этих минимумов находит максимум => это (-1) – это maxmin, нижняя цена игры в чистых стратегиях и достигается она при стратегии a₂

 

Для второго игрока:

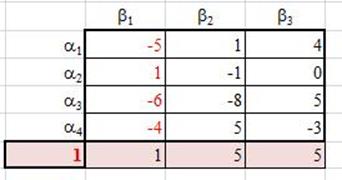Он ищет максимальный проигрыш для каждой стратегии. Следовательно, минимум максимального проигрыша достигается в (1) – это верхняя цена игры. Достигается при стратегии b₂ второго игрока.

И эта пара стратегий a₂ b₂ это пара maxmin

Если они её выберут, то второй игрок проиграет (1), а первый игрок выиграет (1)

Второй игрок проиграет столько, сколько он и предполагал, а первый игрок получит результат лучше.

Существует ли равновесие?

Нет, не существует. Т.к. нижняя цена игры не равна верхней цене игры.

б) Найдите равновесие в смешанных стратегиях игры G. Укажите значение игры, оптимальные стратегии игроков, ожидаемые выигрыши игроков при оптимальных стратегиях.

Запишем задачу линейного программирования для определения смешанной стратегии в матричной игре

Смешанная стратегия первого игрока – Xi и соответствует строкам

Х= (Хi | iÎ 1,4)

Смешанная стратегия второго игрока – Yi и соответствует столбцам

Y = (Yj | jÎ 1,3)

- ожидаемый выигрыш первого игрока при условии, что второй игрок играет свою чистую стратегию с номером bj

V – это искомый maxmin

V→max

Sxi=1

xi≥0,

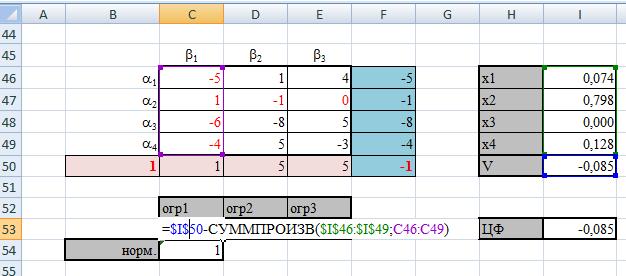
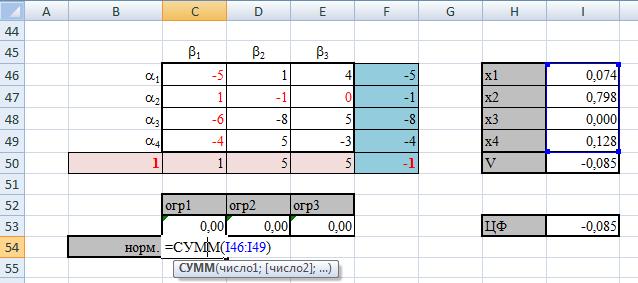
Поиск решения:

ЦФ → max

Изменяя: (Х1, Х2, Х3, Х4, V)

Ограничения: (огр1, огр2, огр3)≤0

                          Норм.=1

                          (Х1, Х2, Х3, Х4)≥0

Параметры: линейная модель, не отриц. значения отключаем.

Видим, что первый игрок должен использовать 1,2,4 стратегии с вероятностями 0,074; 0,798; 0,128 соответственно.

Для второго игрока теневые цены дают смешанную стратегию.

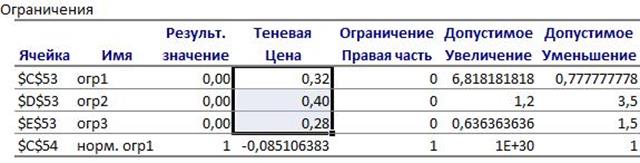
0,32

0,40

0,28

å=1

Значение игры = -0,085

Оптимальные стратегии игроков

Ожидаемые выигрыши игроков

Выигрыш первого игрока = - 0,085

Выигрыш второго игрока = + 0,085

ð первый игрок проигрывает меньше чем в чистых стратегиях, а второй игрок выигрывает больше.