Исследование электрических цепей второго порядка

Министерство образования Российской Федерации

Рыбинская государственная авиационная технологическая академия им. П.А. Соловьева

Кафедра "Радиоэлектронных и телекоммуникационных систем"

Факультет "радиоэлектроники и информатики"

Расчетно-графическая работа

По курсу «Общая электротехника и электроника»

На тему" Исследование электрических цепей второго порядка"

Студент гр. ВР-07                                                                     Воронов Е.А

Преподаватель:                                                                          Станевко В.Н

Дата сдачи:

Подпись:

Рыбинск 2009

Выполнить электрический  анализ цепи при гармоническом входном воздействии:

1. Определить величину нагрузки для заданной цепи, при которой в нее будет передаваться максимум  мощности на заданной частоте, принять Rн=|Z22´|

2. Рассчитать заданную электрическую цепь с учетом п.1при гармоническом входном сигнале uвх=Umcosωt

3. Оценить точность расчета методом баланса мощностей. Погрешность расчета не должна превышать 0,1%.

4. По результатам расчета построить векторную диаграмму. На векторной диаграмме проверить выполнение законов Киргофа для заданной схемы.

1. Определить величину нагрузки для заданной цепи, при которой в нее будет передаваться максимум  мощности на заданной частоте, принять Rн=|Z22´|.

Исходные данные:

f, кГц	R1, Ом	R2, кОм	С, мкФ	L, мГн	Um, В
5	2	2	1,0	1,0	10

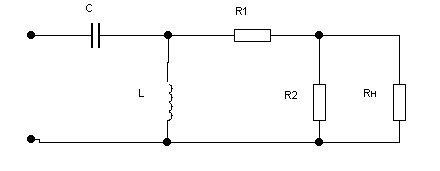
                                     Рис.1 Исходная схема.

1.Для определения величины нагрузки Rн, перемкнем клеммы 1-1´  и найдем сопротивление цепи относительно клемм 2-2´.

Представим схему для определения Rн в комплексной форме.

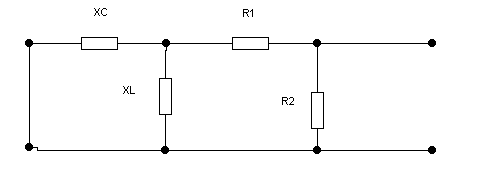
                             Рис.2 Схема в комплексной форме.

   Величину резонансной частоты находим следующим образом  ω=2πƒ      (1)

ω=2πƒ=2 ·3,14 ·5 =6,28 ·5 000 Гц=31 400 рад ;

Хс= j · Хс= - j ·(1/ ωС);                                                                                           (2)

XL=  j  · XL= j  ·ωL;                                                                                                 (3)