Исследование электрических цепей второго порядка, страница 2

   Подставим значение резонансной частоты в формулу (2) и(3) и найдем  Хс и XL:

Хс=-31,831j Ом;

XL=31,416j Ом;

Используя эквивалентные преобразования, найдем величину сопротивления Zэкв.

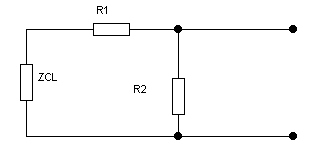
                     Рис.3 Эквивалентное преобразование Хс  и XL.

R1´= Хс · XL/ Хс+ XL = (L/C)/ j(ωL-(1/ωC));                                                          (4)

   Подставим численные значения в формулу (4) и получим

R1´=(-31,831/31,416)/- j(0,415)= j2409,6451;

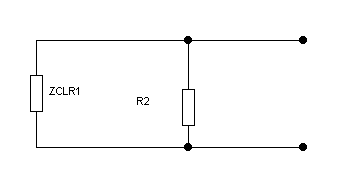
             Рис.4 Эквивалентное преобразование ZCL и  R1.

ZCLR1= ZCL + R1;                                                                                               (5)

     Подставим численные значения в формулу (5) и получим

ZCLR1= j2409,6451+2;

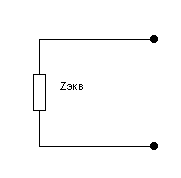
                    Рис.5 эквивалентное преобразование ZCLR1 и R2.

Zэкв=Z22'= ZCLR1 · R2/ ZCLR1+ R2;                                                                      (6)

     Подставим численные значения в формулу (6) и получим

Zэкв =2000(j2409,6451+2)/( j2409,6451+2002)= 2000(j2409,6451+2)( j2409,6451-2002)/( j2409,6451+2002)( j2409,6451-2002)=1,184*10³+982,114i; 

Найдем модуль величины Zэкв, который будет равен сопротивлению нагрузки Rн.

  Rн= |Z22'|= √1,184*10³+982,114i =1,583*10³ Ом

2. Рассчитать заданную электрическую цепь с учетом п.1при гармоническом входном сигнале uвх=Umcosωt.

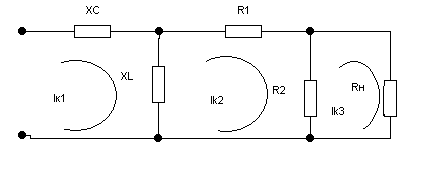
                               Рис.6 Схема контурных токов.

Будем использовать метод контурных токов:

Uвх=Iк1· Хс + XL(Iк1-Iк2);                                                                                         (7)

0= Iк2· R1+ XL(Iк2-Iк1)+ R2(Iк2-Iк3);                                                                          (8)

0= Rн · Iк3+ R2(Iк3- Iк2);                                                                                           (9)

Uвх=Iк1(Хс+ XL)- Iк2· XL;                                                                                       (10)

0= - Iк1· XL+ Iк2(R1+ XL+ R2)- Iк3· R2;                                                                  (11)