Моделирование выборки из стандартного распределения, страница 5

4.2) Определить функцию Колмогорова K(x) и построить её график.

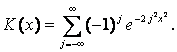
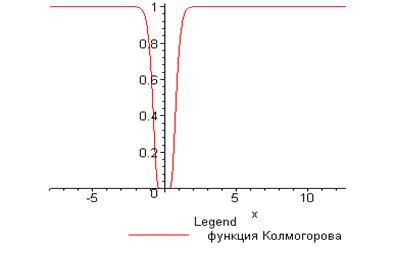
4.3) Для вероятности ошибки a=0,05 решить графически уравнение 1-K(x)=a.

 

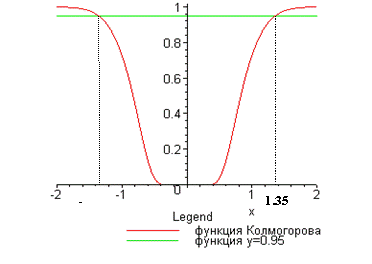4.4) Построить коридор для функции распределения F_n(x)-|z_a|/Ön < F_x(x) < F_n(x)+ |z_a|/Ön, где K(z_a)=1-a.

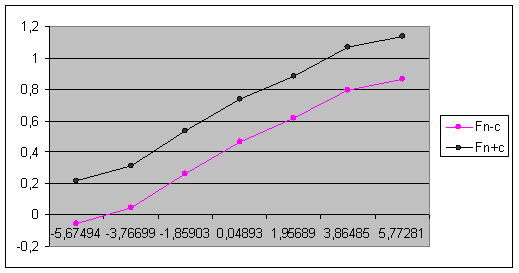
Выше мы нашли, что |z_a|=1.35, значит с =|z_a|/Ön=1,35/10=0,135. Отсюда строим графики функций F_n+c и F_n-c по таблице:

Задание 5.

Интервальное оценивание параметров.

Для нормального распределения случайной величины вычислить с вероятностью g=0,95 доверительный интервал для математического ожидания при неизвестном среднеквадратическом отклонении и с g=0,9 доверительный интервал для среднеквадратического отклонения.

Доверительным называют интервал, который с заданной надежностью покрывает оцениваемый параметр.

Доверительным интервалом с надежностью g  математического ожидания a нормально распределенной с.в. x  при неизвестном среднеквадратическом отклонении s служит интервал  , где  - точность оценки, t_g – табличное значение.

Из таблицы значений функции Ф(t) получаем, что 1.9<t<2.0. Возьмем t=1.95, тогда

Доверительный интервал для М при неизвестном D с вероятностью 0,95 (-0,4883049;0,803413);