Моделирование выборки из стандартного распределения, страница 4

где  , x_l– левая граница медианного интервала; h – шаг группировки; - число элементов в медианном интервале.

Задание 4.

Оценка функции распределения.

4.1) В качестве эмпирической функции распределения F_n(x), n=100 использовать функцию накопления частот, а в качестве F_x(x) берется функция нормального распределения с параметрами а и s². Построить графики F_n(x) и F_x(x) в одной системе координат.

Таким образом,

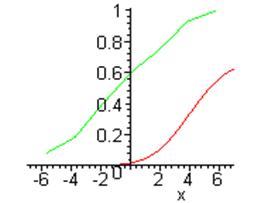
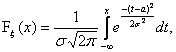
а F_n(x) задается таблицей: