Интервал [-6,62892; 6,726784] разбиваем на N подынтервалов [ai; bi], где a1= -6,62892, bN=6,726784. Затем подсчитываем число ni элементов выборки, попавших в каждый подынтервал, то есть частоту попадания статистических данных в каждый подынтервал.
|
ai |
bi |
ni |
|
-6,62892 |
-4,72096 |
8 |
|
-4,72096 |
-2,81301 |
18 |
|
-2,81301 |
-0,90505 |
40 |
|
-0,90505 |
1,00291 |
60 |
|
1,00291 |
2,910868 |
75 |
|
2,910868 |
4,818826 |
93 |
|
4,818826 |
6,726784 |
100 |
|
x |
|
|
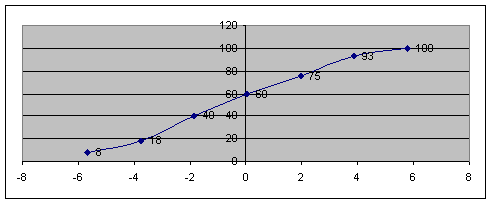
-5,67494 |
8 |
|
-3,766985 |
18 |
|
-1,85903 |
40 |
|
0,04893 |
60 |
|
1,956889 |
75 |
|
3,864847 |
93 |
|
5,772805 |
100 |
Задание 3.
Определить выборочное среднее `x, выборочную медиану , выборочную дисперсию S2, выборочное среднее квадратичное отклонение S, выборочные моменты 3 A3 и 4 A4 порядков, выборочный коэффициент асимметрии A и выборочный коэффициент эксцесса E.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.