Определение абсолютной скорости и кориолисово ускорения точки

Задание К.7. Определение абсолютной скорости и кориолисово  ускорения точки.

Точка М движется относительно тела D. По заданным уравнениям относительного движения точки М и движения тела D определить для момета времени t = t₁ абсолютную скорость и кориолисово ускорение.

Дано :   ОМ = S_r = S_r (t) = 25 sin 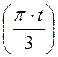 см.

               рад.

             t_{1 =} 4 c.

             а = 25 см.

Найти: V = ?, а_с=?.

 По условию на рисунке №1 дана пластина, которая вращается вокруг оси О₁,      по закону                рад. В верхней части пластины имеется канал АВ, по этому каналу из точки О движется точка М по закону: 

ОМ = S_r = S_r (t) = 25 sin 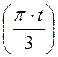 см.

Необходимо определить абсолютную скорость точки М и кориолисово ускорение при t_{1 =} 4 c.

Решение.

1)  Движение точки М можно рассматривать как сложное: движение точки М по отношению к телу D и вместе с телом D.

2)  Проведем подвижную систему координат Х, У, Z, с началом в точке О,    соединив ее с телом D.

3)  Рассмотрим относительное движение т. М (остановим тело D) – оно будет прямолинейным по каналу АВ, по известному закону:

           ОМ = S_r = S_r (t) = 25 sin 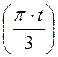 см.

Найдем положение точки М при t₁ = 4 c.

ОМ = 25 sin 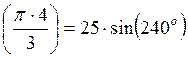= - 25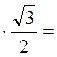-21,65 см.

Отрицательный знак показывает, что положение точки М, при t₁ = 4 c. находится в отрицательной части оси Х. Вследствие этого изменим принятое по условию положительное положение точки М, на отрицательное положение получившееся в ходе основного расчета. (Рис. №1).

4) Найдем абсолютную скорость точки М, как геометрическую сумму относительно и переносной скоростей.

а) Определим V_r по формуле:

=

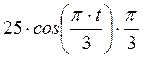
При t₁ = 4 c.

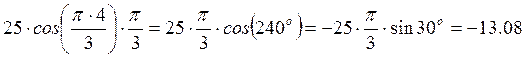 см/с.

Отрицательный знак у величины V_r показывает, что вектор  направлен в сторону убывания S_r т.е вектор лежит непосредственно на оси Х и направлен в сторону отрицательного значения данной оси (Рис.№1).

5) Рассмотрим переносное движение системы (тела D):

   оно является вращением тела D вокруг оси О₁ по закону:

 рад.

а) Найдем , а также определим :

= =4t – 0.5 рад/с

 = = 4 рад/с²

б) Определим данные величины при t ₁= 4 c.

    =4 4 – 0.5 = 15,5 рад/с

    = = 4 рад/с²

Покажем на рисунке  и , а так же покажем вектор  (вектор  параллелен оси OZ).

6) Рассмотрим переносное движение т. М (остановим «точку М»). Это будет движение по окружности с центром в т. О₁ и радиусом R_e.

Соединим точку М с центром О₁, это и будет данный радиус R_e.

Из точки М на нижнюю часть пластины опустим перпендикуляр МС. Вследствие проведенных действий на рисунке №1 образовался прямоугольный треугольник СМО₁, гипотенузой которого является  R_e= О₁М.

Из теоремы Пифагора определяем  R_e.

R_e =см.

Так как радиус траектории движения мы определили, то можем показать и саму траекторию движения точки М (рис.1). Траектория точки М представлена в виде окружности с радиусом R_e = 53 см.

7) Определим модуль переносной скорости при t₁=4 c.

  V_е =  см/с.

Покажем вектор  на рисунке №1. Данный вектор  направлен по касательной к окружности (траектории движения) в сторону вращения тела. Также данный вектор является перпендикуляром к радиусу траектории движения.  

8) Найдем абсолютную скорость и кориолисово ускорение т.М при t₁=4c.    

Из теории известно:

Так как вектор   не перпендикулярен , то величину   найдем аналитическим путем, т.е. проецированием на оси X,Y,Z. (Рис.1)

V =

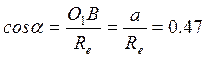
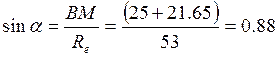
V =  cм/с.

Покажем вектор  на рисунке №1.

9) Определим кориолисово ускорение .

Векторы параллелен оси ОZ, а вектор  лежит на оси ОX, следовательно между этими векторами образуется угол в 90^о, т.е. .  

а_с = см/с.

Вектор параллелен оси Y и направлен в сторону отрицательного значения данной оси, т.е. направлен вниз. (Рис.1).

Ответ: V = 813,624 cм/с;

            а_с = 405,48 см/с.