Спектральная плотность входного сигнала, амплитудный и фазовый спектр, ширина спектра, страница 4

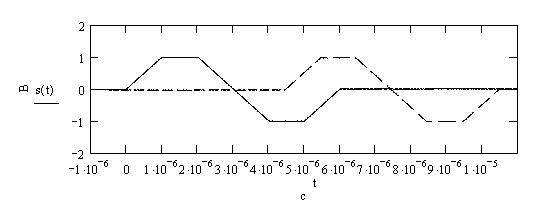
Рисунок 1.5 – Смещение сигнала на  при

Корреляционная функция для входного сигнала, сдвинутого на  при , определяется следующей суммой интегралов:

.

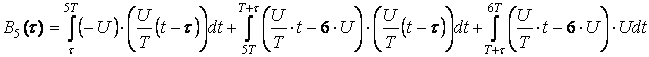В результате вычислений получим:

.

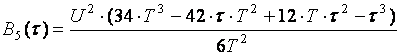Подставим исходные данные:

.

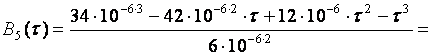
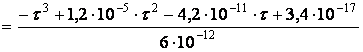На рисунке 1.6 представлены графики входного сигнала и его копии, смещенной на  при :

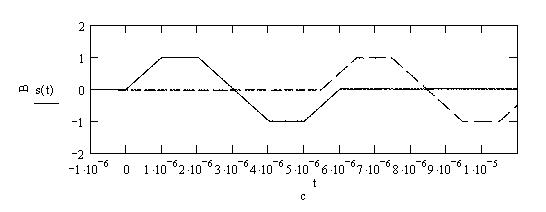
Рисунок 1.6 – Смещение сигнала на  при

Корреляционная функция для входного сигнала, сдвинутого на  при , определяется следующим интегралом:

.

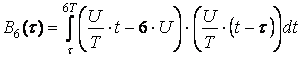В результате вычислений получим:

.

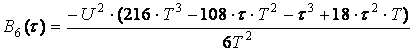Подставим исходные данные:

.

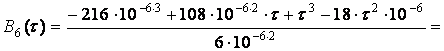
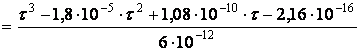Обобщим полученные данные для получения выражения корреляционной функции на интервале :

.

График корреляционной функции представлен на рисунке 1.7:

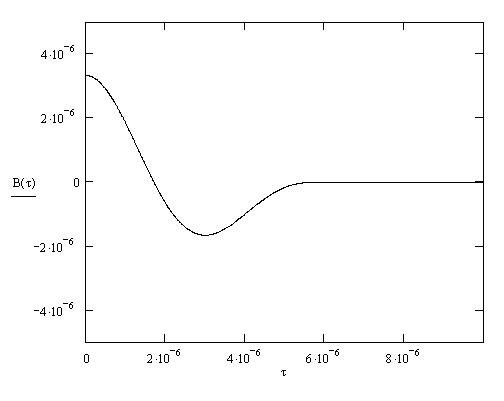
Рисунок 1.7 – Корреляционная функция входного сигнала

1.2 Спектральный анализ входного сигнала

Представим входной сигнал аналитически с использованием функции включения:

.

Для удобства последующих вычислений преобразуем это выражение:

.

Выполним преобразование Лапласа:

.

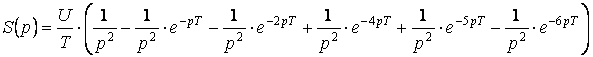Так как площадь, ограниченная графиком входного сигнала и осью абсцисс, конечна, то входной сигнал является абсолютно интегрируемым и для нахождения спектральной плотности достаточно перейти от p к jω:

.

Амплитудный спектр есть модуль спектральной плотности:

.

Найдем ширину спектра; согласно амплитудному методу определения ширины спектра Dw на уровне 0,1×|S(w)|, как показано на рисунке 1.8: