Спектральная плотность входного сигнала, амплитудный и фазовый спектр, ширина спектра, страница 2

Задание на курсовую работу

РАССЧИТЫВАЕМЫЕ ХАРАКТЕРИСТИКИ

1. Спектральная плотность входного сигнала, амплитудный и фазовый спектр, ширина спектра.

2. Частотный коэффициент передачи цепи, АЧХ, ФЧХ.

3. Импульсная и переходная характеристики цепи.

4. Спектральная плотность выходного сигнала, амплитудный и фазовый спектр, ширина спектра.

5. Выходной сигнал.

ИСХОДНЫЕ ДАННЫЕ

Схема электрическая принципиальная:

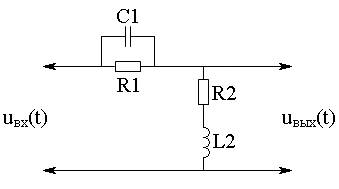
Входной сигнал:

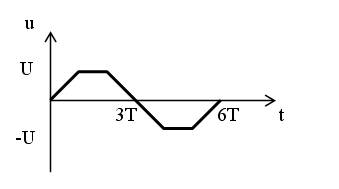
Параметры элементов цепи и сигнала:

Вариант	Параметры
0	C1, нФ	1
	C2, нФ	1
	L1, мГн	1
	L2, мГн	1
	R1, кОм	1
	R2, кОм	1
	U, В	1
	T, мкс	1

Содержание

1 Анализ входного сигнала                                                                             5

    1.1 Корреляционная функция                                                                      5

    1.2 Спектральный анализ входного сигнала                                                      12

2 Анализ цепи                                                                                                 15

3 Анализ выходного сигнала                                                                                  21

4 Программное моделирование цепи и сигнала                                                   26

5 Выводы                                                                                                        32

Список литературы                                                                                        33

1 Анализ входного сигнала

1.1 Корреляционная функция входного сигнала

Найдем корреляционную функцию входного сигнала. Для вещественного сигнала s(t), имеющего конечную энергию на бесконечном интервале времени, автокорреляционная функция определяется следующим образом:

.

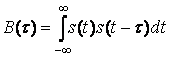Входной сигнал можно определить при помощи кусочно-заданной функции:

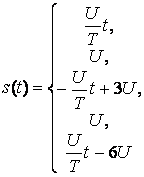
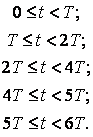
На рисунке 1.1 представлены графики входного сигнала и его копии, смещенной на  при :

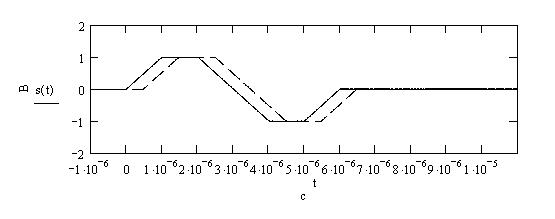
Рисунок 1.1 – Смещение сигнала на  при

Корреляционная функция для входного сигнала, сдвинутого на  при , определяется следующей суммой интегралов: