Модель общего экономического равновесия (Модель Эрроу-Дебре) и ее обобщения

Глава одиннадцатая. Модель общего экономического равновесия (Модель Эрроу-Дебре) и ее обобщения.

11.1 Сфера призводства модели Эрроу-Дебре (МЭД). Функция рыночного равновесия и ее свойства.

Сферу производства МЭД составляют фирмы. В МЭД фигурирует  фирм  и   продуктов . Каждая фирма  выпускает продукты и затрачивает ресурсы. Если продукт   выпускается фирмой  в количестве  единиц, то, если продукт, затрачивается фирмой   в качестве ресурса в количестве  единиц, то .  Вектор                           

                             ,

где   – технологическое множество фирмы .

Технологическое множество   удовлетворяет следующему условию:

(1.1) Для всех   множество  ограничено и замкнуто и , т.е. фирма  может ничего не затрачивать и ничего не выпускать. Разные фирмы   могут выпускать и затрачивать разные продукты. Сумма (по Минковскому):

называется технологическим множеством МЭД. Оно удовлетворяет условию:

(1.2)  -выпуклое множество.

Пусть  вектор цен в МЭД. Каждая фирма , максимизирует свою прибыль

                                                                                                 (1)

при условии, что

                                        .                                                           (2)

Решение задачи максимизации прибыли фирмы   обозначим символом . Решение  всегда существует, ибо множество  ограничено и замкнуто. Решение  называется локальным рыночным равновесием фирмы  или предложением фирмы  . Сумма 

                                                                               (3)

называется совокупным предложением (рыночным предложением).

Пример.      

Пусть .

Пусть   

Пусть вектор рыночных цен . Задача максимизации прибыли   фирмы  в этом случае имеет вид                                                                    

при наличии ограничений , , .

Тогда имеем        

                    (см. рис. 11.1).            

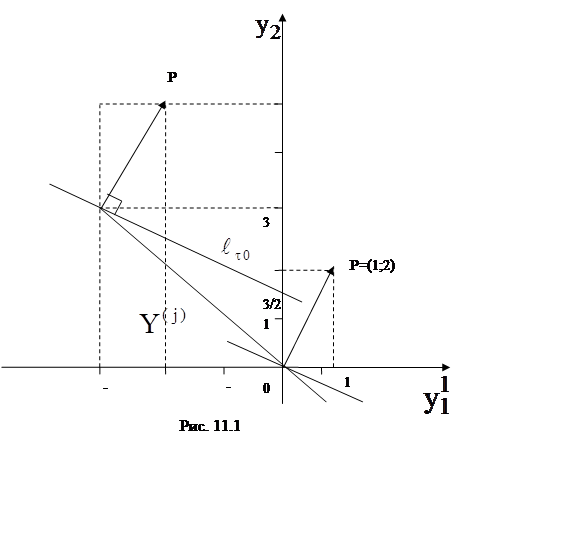Прямая –изопрофита, проходящая через точку  , максимизирующую прибыль  фирмы , т.е.

                     .

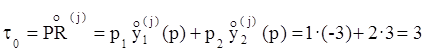Предложение  фирмы  есть функция, однородная нулевой степени своей векторной переменной , ибо                                                          

                                ,                                                                   (4)                            

где , поскольку обе задачи (задача (1), (2) и задача   при условии (2)) имеют одно и то же множество максимальных решений.

Из равенств (3) и (4) следует, что

                                                        .                                                  (5)                               

11.2 Сфера потребления МЭД. Функция рыночного спроса                 и ее свойства.

Сферу потребления МЭД составляют потребители (например, домашние хозяйства). В МЭД фигурирует  потребителей . Каждый потребитель  максимизирует свою функцию полезности  при наличии бюджетного ограничения  , где - доход потребителя . Таким образом, каждый потребитель  решает задачу максимизации

                                                                                                     (1)

 при условии, что

                                   , .                                                              (2)

Решение задачи максимизации потребителя  обозначается символом  и называется локальным рыночным равновесием потребителя  или спросом потребителя . Сумма

                                                                                   (3)

называется совокупным спросом (рыночным спросом).

Функция полезности  удовлетворяет следующим условиям

(2.1) Функция  имеет непрерывные частные производные по всем переменным .

(2.2) Множество   является строго выпуклым. Каждый потребитель   имеет запас продуктов   такой, что .