(2.3)
Каждый потребитель ![]() получает долю
получает долю ![]() прибыли
прибыли ![]() фирмы
фирмы ![]() и
и ![]() .
.
Доход
![]() потребителя
потребителя ![]() равен
сумме
равен
сумме ![]() , где
, где ![]() ,
,
11.3 Формулировка общего экономического равновесия и формулировка теоремы о его существовании.
Общее экономическое равновесие ( конкурентное равновесие) есть набор векторов
![]() (1)
(1)
удовлетворяющих условиям:
1) вектор![]() и
и ![]() ,
,
вектор ![]() называется вектором цен общего
экономического равновесия МЭД;
называется вектором цен общего
экономического равновесия МЭД;
2)
вектор![]() , есть локальное рыночное равновесие
фирмы
, есть локальное рыночное равновесие
фирмы ![]() , т.е. решение задачи максимизации прибыли
, т.е. решение задачи максимизации прибыли ![]() фирмы
фирмы![]() при ценах
при ценах ![]()
![]()
![]()
при условии, что
![]()
3)
вектор ![]() есть локальное равновесие потребителя
есть локальное равновесие потребителя![]() , т.е. решение задачи максимизации функции
полезности
, т.е. решение задачи максимизации функции
полезности![]() при ценах
при ценах ![]()
![]()
при условии, что
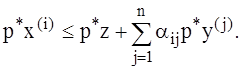
4) имеет место следующее векторное неравенство:
![]()
(которое
означает отсутствие в МЭД дефицита) и условие дополняющей (нежёсткости) ![]()
где
![]()
Условие дополняющей (нежесткости) в развёрнутом виде выписывается так:
![]()
Это
условие означает, что если![]() то обязательно
то обязательно![]() ,
,
если
же ![]() , то цена
, то цена ![]()
При выполнении условий (1.1), (1.2), (2.1), (2.2), (2.3) существует общее экономическое равновесие (1) (теорема Эрроу – Дебре).
1)
пространство продуктов ![]() ;
;
2)
два потребителя ![]() и
и ![]() с
характеристиками:
с
характеристиками:
потребитель
![]() имеет начальный запас
имеет начальный запас ![]() и функция полезности
и функция полезности ![]() ;
;
3) фирма F имеет технологическое множество
Y = {(y1, y2) ôy1< 1 и y2 £ y1/(y1-1)};
4)
доли потребителей в прибыли фирмы равны 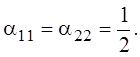
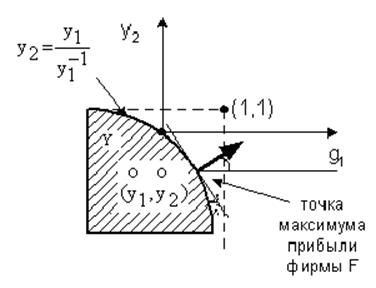
Технологическое множество Y изображено на рис. 11.2.
Пусть вектор цен ![]()
![]() Очевидно,
в точке
Очевидно,
в точке ![]() нормаль к линии
нормаль к линии ![]() имеет
тангенс угла наклона y1/y2 (см. рис. 11.2). Дифференцируя равенство
имеет
тангенс угла наклона y1/y2 (см. рис. 11.2). Дифференцируя равенство ![]() , получаем
, получаем ![]() , так
что тангенс угла наклона нормали равен
, так
что тангенс угла наклона нормали равен ![]() .
Следовательно, локальное равновесие
.
Следовательно, локальное равновесие ![]() фирмы определяется как
решение задачи на условный экстремум:
фирмы определяется как
решение задачи на условный экстремум: ![]() при
условии, что
при
условии, что 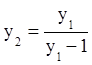 .
.
Тогда ![]() и
и
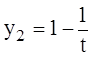 .
.
Функция предложения фирмы –
это 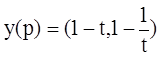 , где
, где ![]() .
.
Рассмотрим поведение первого
потребителя ![]() Его доход
Его доход ![]() равен
равен 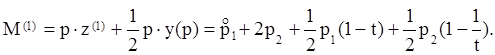
Он максимизирует функцию
полезности ![]() при бюджетном ограничении
при бюджетном ограничении ![]() С помощью множителей Лагранжа получаем, что
для выбора
С помощью множителей Лагранжа получаем, что
для выбора ![]() , максимизирующего полезность, выполнено
равенство
, максимизирующего полезность, выполнено
равенство ![]() . Таким образом,
. Таким образом, ![]() поэтому
поэтому
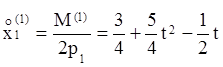 и
и 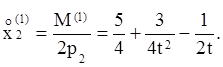
Следовательно, функция спроса
первого потребителя ![]()
![]() это
это 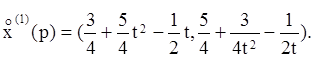
Перейдём ко второму
потребителю ![]() . Его доход равен
. Его доход равен 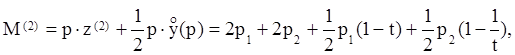 и
свою функцию полезности
и
свою функцию полезности ![]() этот потребитель
максимизирует при бюджетном ограничении
этот потребитель
максимизирует при бюджетном ограничении ![]() . Вновь
используя множители Лагранжа, получаем, что для набора, максимизирующего
полезность, выполнено равенство
. Вновь
используя множители Лагранжа, получаем, что для набора, максимизирующего
полезность, выполнено равенство ![]() . Следовательно,
. Следовательно, ![]() Отсюда вытекает, что
Отсюда вытекает, что 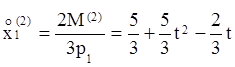 и
и 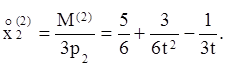
Следовательно, функция спроса второго потребителя выглядит так:
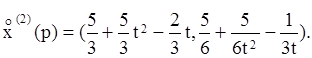
Функция
избыточного спроса ![]() для этой МЭД задается формулой
для этой МЭД задается формулой
![]() =
=
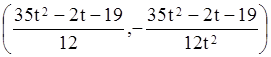 .
.
Таким образом, ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() .
.
Решая это квадратное
уравнение и учитывая, что ![]() , получаем
, получаем
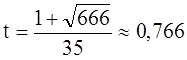 .
.
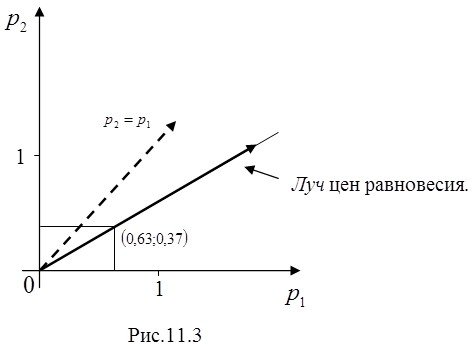
Так как ![]() , то цены суть
, то цены суть ![]() .
.
Соответствующий луч равновесных цен в плоскости цен изображен на рис. 11.3
 |
![]()
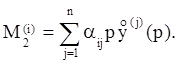
Спрос
![]() потребителя
потребителя ![]() есть
однородная нулевой степени своей векторной переменной
есть
однородная нулевой степени своей векторной переменной ![]() ,
ибо
,
ибо ![]() (4)
(4)
где ![]() поскольку
обе задачи (задача (1), (2) и задача
поскольку
обе задачи (задача (1), (2) и задача ![]() (1)
(1)
при условии, что
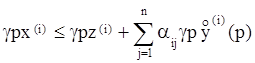 (5)
(5)
имеют одно и то же множество решений.
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.