Новосибирский государственный
архитектурно-строительный университет (Сибстрин)
Кафедра строительных машин,
автоматики и электротехники
Индивидуальное задание №2
Вариант № 0
РАСЧЕТ И АНАЛИЗ ОДНОФАЗНОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА
Выполнила студентка гр. 219 Б
Вепрева Анна
Проверила ст. преподаватель
Осипова Л.Б.
Новосибирск-2008
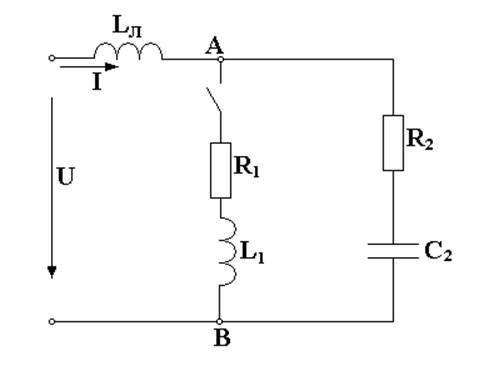 U
= 500 B
U
= 500 B
ƒ= 50 Гц
LЛ = 25 мГн
R1 = 12 Ом
R2 = 18 Ом
L1 = 151 мГн
C2 = 119 мкФ
I. а) Ключ разомкнут, до резонанса напряжений.
Полное комплексное сопротивление цепи:
Z= R2 + jXLл – jXС2
Реактивные сопротивления катушки и конденсатора :
XLл = w·LЛ = 2πƒLЛ = 314,16*·25·10-3 = 7,85 Ом
XC2 = 1/(w·С2) = 1/(314,16·119·10-6) = 26,75 Ом
Z = 18 + j(7,85 – 26,75) = 18 – j18,9 = 26,1e-j46,4° Ом
Ток в последовательной цепи :
I = Uвх/Z = 500/26,1e-j46,4° = 19,16 e j46,4° =
=19,16·cos 46,4° + j19,16·sin 46,4° = 13,21 + j13,88 A
Падения напряжения на участках цепи:
UR2 = I·R2 = 19,16ej46,4°·18 = 344,88 e j46,4°В
UC2 = -jXC2·I = 26,75· e-j90° 19,16e j46,4°· = 512,53e-j43,6° B
ULл = jXLл·I = 7,85ej90°·19,16e j46,4° = 150,41e j136,4° B
S = U·I* = 500·(13,21 – j13,88) = 6605 – j6940 BA = 9580,7 e-j46,4° BA
Векторная диаграмма: МU= 50В/см; МI = 4А/см
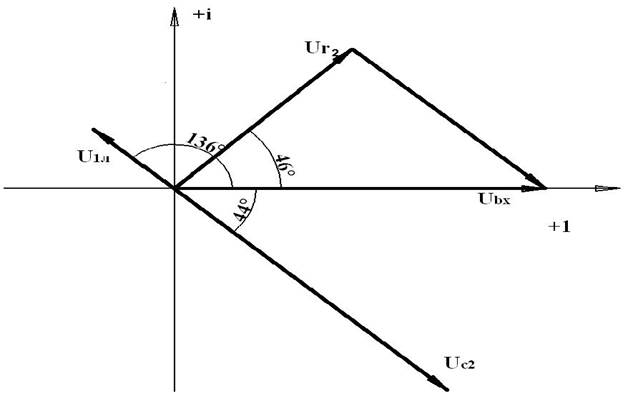
I. б) Ключ разомкнут, резонанс напряжений.
Резонанс напряжений выражается в том, что полное сопротивление контура становится наименьшим и равным активному сопротивлению, а ток становится максимальным.
Условием резонанса напряжений является равенство индуктивного и емкостного сопротивлений для токагенератора:
XLл = XC2
w·LЛ = 1/(w·C2P) =>C2P = 1/(w2·Lл) = 405,7 мкФ
Ток в последовательной цепи во время резонанса напряжений:
IP = U/(R2 + jXL – jXC2р) = U/R2 = 500/18 = 27,78 A
Падение напряжения на участках цепи:
UXL = IP·jXLл = 27,78·7,85ej90° = 218,06ej90°B
UC2 = -jXC2р·IP = 27,78·7,85e-j90° = 218,06e-j90° B
UR2 = R2·IP = 18·27,78 = 500 B
Полная мощность :
S = I*·U = 500·27,78 = 13890 Вт или по другой формуле
S = R2·IP2=18 * 27,782= 13891 Вт
Векторная диаграмма: МU= 50В/см; МI = 4А/см
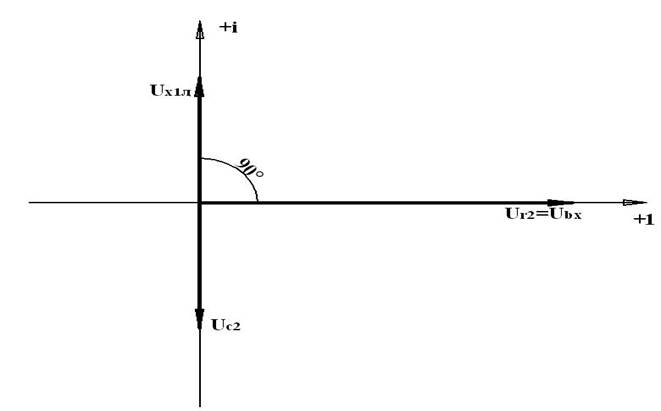
II. а) Ключ замкнут, до резонанса токов.
Реактивное сопротивление катушки в 1-й ветви:
XL1 = w·L1 = 2πƒL1 = 314,16*·151·10-3 = 47,44 Ом
Полные комплексные сопротивления 3-х ветвей:
ZЛ = jXLл = 7,85 ej90° Ом
Z1 = R1 + jXL1 = 12 + j47,44 = 48,93 ej75,8° Ом
Z2 = R2 – jXC2 = 18 – j26,75 = 32,24 e-j56,06° Ом
Эквивалентное сопротивление параллельных ветвей
ZАВ = Z1* Z2 /( Z1+ Z2) =
=(48,93ej75,8° *32,24e-j56,06°) / (12 + j47,44+18 – j26,75 ) =
= (1577,5* e j19,74)/(30+ j 20,69) =(1577,5* e j19,74)/(36,44* e j34,6) = =43,29* e –j14,86=43,29*cos(-14,86) + j43,29*sin(-14,86)=41,84– j11,1 А
Общее сопротивление схемы:
Zобщ = ZАВ + ZЛ = 41,84– j11,1 + j7,85 = 41,84 – j3,25 = 41,97e-j4,44° Ом
Ток в неразветвленной части цепи:
Iобщ = U/Zобщ = 500/41,97e-j4,44° = 11,91ej4,44° = 11,87+j0,92 A
Напряжение на зажимах параллельных ветвей:
UAB = Iобщ·ZAB = 11,91ej4,44°·43,29e-j14,86° = 515,58e-j10,42° B
Токи ветвей:
I1 = UAB/Z1 = 515,58e-j10,42°/48,93ej75,8°=10,54e-j86,22° = 0,69 – j10,52 A
I2 = UAB/Z2 = 515,58e-j10,42° /32,24e-j56,06° = 16ej45,64° A
Полная мощность:
S=I*·U = 500·(11,87 – j0,92) = 5935 – j460 = 5952,8 e-j4,44° BA
PQ
Р -активная мощность (Вт) , Q– реактивная мощность (ВАр)
Падение напряжения в линии:
UZл = jXLл·I = 11,91ej4,44°·7,85ej90° = 93,45ej94,44° B
Векторная диаграмма: МU= 50В/см; МI = 2А/см
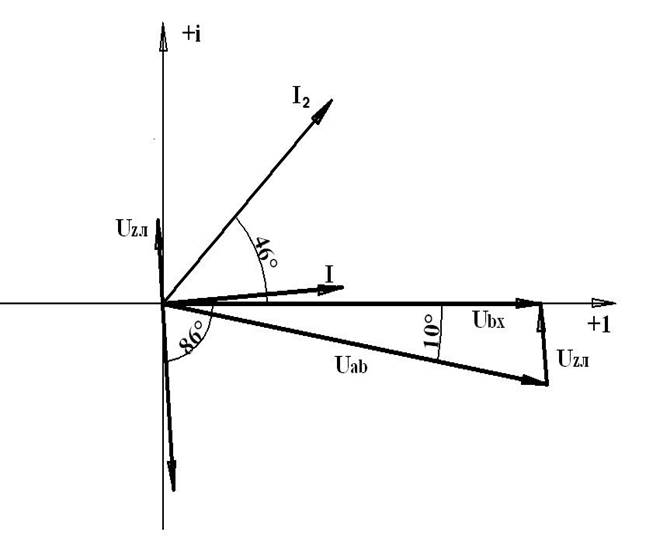
II. б) Ключ замкнут, резонанс токов.
Физический признак резонанса токов –минимальный ток, потребляемый источником ( ток в линии ). Явление полезное в силовых цепях, т.к. уменьшаются потери мощности DP=Rл* Iл2.
Условие резонанса токов: реактивная проводимость ветви с катушкой должна быть равна реактивной проводимости ветви с конденсатором:
BL = BC [ Сименс ]
XL1/(R21 + X2L1) = XC2/(R22 + X2C2р)
Решаем квадратичное уравнение относительно XC2р
47,44/(144 + 2250,55) = XC2р/(324 + X2C2р)
15370,56 + 47,44X2C2р = 2394,55XC2р
X2C2р – 50,48XC2 + 324 = 0
D = 2548,23 – 1296 = 1252,23
X'C2 = 42,93 Ом
X"C2 = 7,55 Ом
Определим емкость конденсатора, обеспечивающую нужное реактивное сопротивление 2-й ветви:
C2P ' = 1/(w·X’C2р) = 1/(314,16*·42,93) = 74,15·10-6 Ф
C2P" = 1/(w·X”C2р) = 1/(314,16*·7,55) = 421,6·10-6 Ф
Новое полное комплексное сопротивление 2-й ветви с новым конденсатором :
Z'2P = R2 – jX'C2р = 18 – j 42,93 = 46,55e-j67° Ом
Z"2P = R2 – jX"C2р = 18 – j 7,55e-j23° Ом= 19,52 e-j22,75°
I'2P = UAB/Z'2P = 515,58e-j10,42°/46,55e-j67° = 11,08ej56,83° =
11,08·cos 56,83° + j11,08 sin 56,83°= 6,06 + j 9,27 A
I"2P = UAB/Z"2P = 515,58e-j10,42°/19,52e-j22,75° = 26,41ej12,33° =
26,41 ·cos 12,33° + j·26,4 sin 12,33° = 25,8 + j 5,64 A
Ток в неразветвленной части цепи (в линии):
I' = I1 + I'2P= 0,69 – j10,52 + 6,06 + j 9,27 A= 6,75 – j 1,25=
6,86е-j10,49°А
I" = I1+ I"2P= 0,69 – j10,52 + 25,8 + j 5,64 A= 26,49 – j 4,88=
26,94е-j10,44°А
Сравнивая ток в линии при наличии во 2-й ветви 3-х различных конденсаторов (11,91ej4,44°А при С2=119 мкФ;
6,86 е-j10,49°А при C'2P = 74,15·10-6 Ф и 26,94 е-j10,44°А при C"2P = 421,6·10-6 Ф ), выбираем конденсатор, обеспечивающий минимальный ток в линии C'2P = 74,15·10-6 Ф.
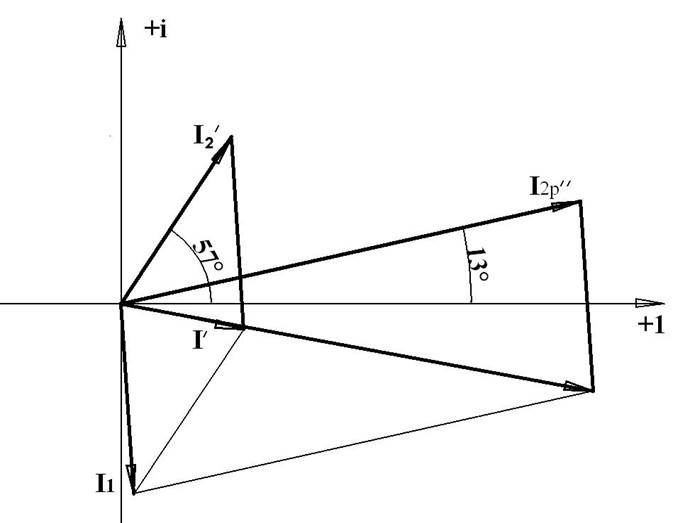
Векторная диаграмма: МU= 50В/см; МI = 2А/см
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.