Одноконтурная цепь из двух последовательно соединенных проводников

§ 2. Одноконтурная цепь.

амая простая задача. Но и её можно разобрать по полочкам. В начале вспомним, что сила тока I будет одна для всех элементов электрической цепи, проводники которой включены последовательно. Напряжение U и мощность P будут разными, в зависимости от сопротивлений включенных в сеть. Это могут быть резисторы, электрические лампочки, нагревательные элементы.

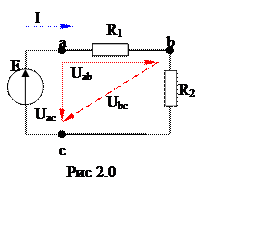За входное условие возьмем сопротивление R₁ равное 3 ом, R₂ – 1 ом, и ЭДС E – 8 вольт.

Цепь состоит из двух последовательно соединенных проводников. Как вы помните при последовательном соединении напряжение на каждом из проводников пропорционально его сопротивлению. Это следует из закона Ома: ; , (2.0) поэтому возникает формула:

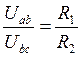. (2.1)

Полное напряжение U между началом первого проводника и концом второго равно сумме этих напряжений. Поэтому .  (2.2)

Если обозначить через R сопротивление всего участка цепи, состоящего из сопротивлений R₁ и R₂ то по закону Ома . (2.3)  Из сравнения двух последних формул легко найти, что . (2.4) Производя подобные рассуждения для 3, 4 и, вообще, n проводников получим, очевидно, следующий результат: . (2.5)

Этим мы доказываем, что сопротивление участка цепи, составленного из последовательно соединенных проводников, равно сумме сопротивлений отдельных проводников. Или коротко: при последовательном соединении проводников складываются их сопротивления.

Из формул (2.3) и (2.4) можно получить силу тока для всей цепи. 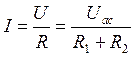 (2.6). В нашем случае U = E. Тогда 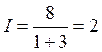ампера. Теперь найдем напряжения между точками ab и bc. Воспользуемся формулами (2.0) вольт,  вольт. Помните, мы говорили, что напряжение U_ac равно напряжению источника ЭДС E? Используя формулу (2.2) получим: вольт. При других входных условиях и другой конфигурации цепи[1] этот результат, общее напряжение цепи равно сумме всех напряжений на проводниках цепи. Соответственно напряжение  на втором проводнике можно было получить по-другому – по формуле (2.2) вычесть из общего напряжения, все известные напряжения цепи. 

Если сумму напряжений представить графическим путем, то для последовательного соединения будет справедлив рисунок (2.1)

Предположим, что необходимо найти напряжение на одном из проводников, если известно только сопротивление проводников и напряжение. В таком случае напряжение на одном из резисторов ветви, состоящей из n последовательно соединенных резисторов, равно приложенному к ветви напряжению, умноженному на сопротивление данного резистора и деленному на сумму сопротивлений всех резисторов, т.е.

                                                                                                                       (2.7)

в нашем  примере:

 и

результаты совпадают с предыдущими расчетами.

Теперь найдем мощность для источника P_ист и потребителя P_потр.

Вопрос, как измениться температура проводника, если через него пропустить электрический ток? Если вспомнить, что паяльник, электроутюг, электрочайник во время своей работы нагреваются, то можно сделать вывод – при прохождении электрического тока через проводник, последний нагревается. Из курса школьной физики можно вспомнить закон Джоуля[2] – Ленца[3]. Количество тепла, выделяющегося в проводнике при прохождении через него электрического ток, прямо пропорционально сопротивлению R проводника, квадрату силы тока I и времени t, в течение которого поддерживается ток в проводнике.

Этот закон можно выразить следующей формулой:

                                                                                   (2.8)

где Q – выделившееся количество тепла, а с – коэффициент пропорциональности. Численно значение этого коэффициента зависит от выбора единиц, в которых проводятся измерения. Если количество тепла измерять в калориях, время – в секундах, сопротивление – в омах, а силу тока – в амперах, то коэффициент с = 0,24. Это означает, что ток в 1 ампер, выделяет в проводнике, имеющем сопротивление 1 ом, за 1 секунду количество тепла, равное 0,24 калории. Таким образом:

                                                 кал                       (2.9)

Вставляя 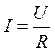в формулу (2.9), получим:  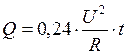калорий. (2.10). Эти две формулы позволяют рассчитать количество тепла, выделяющегося в отдельных проводниках, соединенных последовательно и параллельно. При последовательном соединении, как в нашем случае, во всех проводниках течет ток одной