Второе начало термодинамики, страница 6

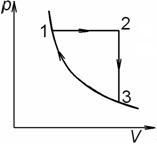
9.  Тепловая машина работает по обратимому циклу 1 – 2 – 3 – 4, в котором 1 – 2 процесс изобарный, 2 – 3 процесс изохорный и 3 – 1 процесс адиабатный. Рабочее вещество – идеальный газ. В расчете на один моль определить теплоты, получаемые газом на каждом этапе, работу за один цикл. Температуры Т₁, Т₂, Т₃ – известны. Найти КПД цикла.

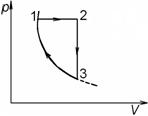
10.  Тепловая машина с идеальным газом в качестве рабочего тела совершает обратный цикл, представленный на диаграмме. Процесс 3 – 1 изотермический. В расчете на один моль рабочего вещества найдите работу, совершаемую машиной за один цикл и КПД цикла.

11. 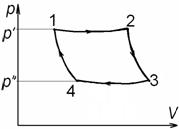 Определить КПД цикла, состоящего из двух изобар 1 – 2, 3 – 4 и двух адиабат 2 – 3 и 4 – 1. Известна величина коэффициента адиабатного расширения (сжатия) .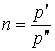

12.  Холодильная машина, работающая по обратному циклу Карно поддерживает в камере температуру 270 К при наружной температуре
300 К. Известно, что  счет теплопроводности в камеру проникает 800 кДж тепла в час. Определить мощность мотора установки, если известно, что она включается в среднем на
15 мин при такой же паузе между включениями.

13.  Холодильная машина, работающая по обратному циклу Карно поддерживает в камере температуру 2 ºС, отводя в окружающую среду, температура которой 30 ºС, 20 МДж тепла в час. Определить совершаемую установкой работу и холодильный коэффициент (отношение количества отведенного тепла к совершенной работе).

14.  Исходя из первого и второго законов термодинамики показать, что внутренняя энергия тела удовлетворяет соотношению .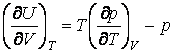

15.  Показать, что внутренняя энергия данной массы идеального газа не зависит от его объема, а зависит лишь от температуры.

16.  Основываясь на основных термодинамических соотношениях, показать, что энтальпия  данной массы идеального газа не зависит от его давления, а зависит только от температуры.

17.  Какую максимальную работу можно получить с помощью идеальной тепловой машины Карно, если в качестве нагревателя выступает некоторая масса металла m с удельной теплоемкостью С и начальной температурой Т₁. Температура окружающей среды, играющей роль холодильника постоянна и равна Т₂.

18.  Используя уравнения Максвелла показать, что .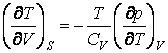

19.  Используя основные термодинамические функции доказать соотношения Максвелла ; ; ; .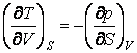

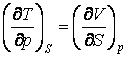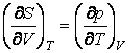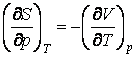20.  Найдите выражение энтропии для 1 моля идеального газа.

21.  Найдите выражение энтропии для 1 моля газа Ван-дер-Ваальса.

22.  Показать, что при стремлении температуры тела к абсолютному нулю его коэффициент теплового расширения и термический коэффициент давления также стремятся к нулю.

23.  Кусок железа массой 100 г, нагретого до температуры 300 ºС, опустили в озеро, температура воды в котором 20 ºС. Теплоемкость железа . Показать, что энтропия системы кусок железа – озеро возрастает в процессе остывания железа.

24.  Кусок льда массой 1 кг, взятый при температуре – 20 ºС был нагрет и расплавлен, а затем при атмосферном давлении полученная вода доведена до кипения и превращена в пар. Найти полное изменение энтропии данной массы вещества.