Второе начало термодинамики, страница 3

т. к. 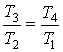, то и .

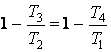Таким образом, .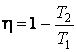

ОТВЕТ: .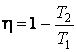

Примечание: если заданы значения  и , то решение получается аналогично.

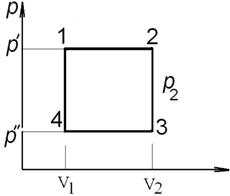ЗАДАЧА 2. Идеальный газ совершает цикл, состоящий из двух изохор и двух  изобар. Найти возможные соотношения между температурами состояний.

          АНАЛИЗ. Цикл задан четырьмя процессами, характер которых достоверно известен: ;;    . Так как газ идеальный, то все его физические свойства в течение цикла остаются постоянными, в том числе и его теплоемкости  и . Задача допускает 2 относительно простых варианта решений.

          РЕШЕНИЕ.

          Вариант 1.

          Считая цикл квазистатическим, применим к нему теорему Клаузиуса . Имеем:

;

.

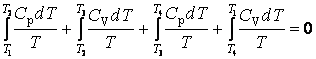
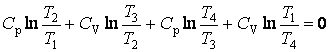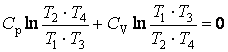После элементарных преобразований получаем:

.

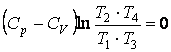Т.к. , то 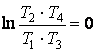 и следовательно .

          Вариант 2.

          Запишем уравнения изобар  и  в координатах :

.

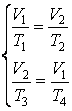Образуем произведение левых и правых частей этих уравнений: 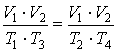, откуда и следует . Условие квазистатического цикла Эдей присутствует в скрытой форме.

          ЗАДАЧА 3. Уильям Томсон предложил схему динамического отопления, в соответствии с которой тепло от топки Q₁ при температуре Т₁ не все поступает в помещение с температурой Т₂, а часть его расходуется на работу тепловой машины, которая приводит в действие холодильную машину, забирающую тепло из окружающей среды с температурой Т₃ и подающую тепло в помещение, при определенных условиях количество тепла Q, полученной при такой системе отопления превысит количество тепла Q₁, получаемое при сжигании топлива в топке. Определить теоретически возможное количество тепла Q, получаемое в режиме динамического отопления, если известны теплотворная способность топлива q и масса сгоревшего за один цикл топлива m.

ДАНО: q m

Q –?

        АНАЛИЗ. При динамическом отоплении часть тепла сгорающего в топке топлива идет на совершение работы тепловой машиной, приводящей в действие холодильную машину. При этом обогреваемое помещение для тепловой машины выполняет роль холодильника. Работа тепловой машины А равна балансу тепла: . Холодильная машина забирает тепло Q₃ из окружающей среды и передает в помещение тепло . Для того, чтобы этот процесс мы иметь место необходимо затратить работу . В идеальном случае  и следовательно .