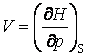 ;
; 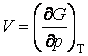
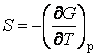 ;
; 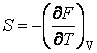 .
.
При решении целого ряда задач оказываются полезными следующие уравнения Максвелла:
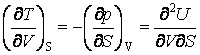

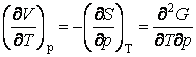
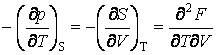 .
.
С помощью уравнений Максвелла можно получить ряд важных соотношений между термодинамическими характеристиками состояния вещества:
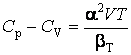 ,
,
где 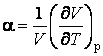 – изобарический температурный
коэффициент теплового расширения;
– изобарический температурный
коэффициент теплового расширения; 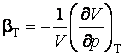 – изотермический
коэффициент сжимаемости. Можно указать интересное соотношение между
температурным коэффициентом объемного расширения
– изотермический
коэффициент сжимаемости. Можно указать интересное соотношение между
температурным коэффициентом объемного расширения 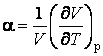 ,
изохорическим температурным коэффициентом давления
,
изохорическим температурным коэффициентом давления 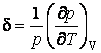 и
изотермическим коэффициентом сжимаемости
и
изотермическим коэффициентом сжимаемости 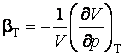 :
:
![]() .
.
Если ввести в рассмотрение адиабатический коэффициент сжимаемости ![]() по определению
по определению 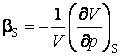 , то можно указать соотношение
следующего вида:
, то можно указать соотношение
следующего вида:
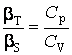 .
.
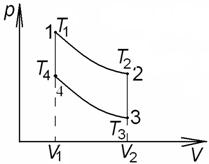
ЗАДАЧА 1. Некоторая масса идеального газа совершает круговой процесс, состоящий из двух адиабат и двух изохор. Определить КПД этого цикла, если известны температуры состояний для одной из адиабат.
|
ДАНО: циклический процесс 1 – 2 – 3 – 4 – 1 (см. диаграмму в осях p, V) T1, T2 (или T3 и T4) |
|
|
АНАЛИЗ.
Предложенная задача связана с анализом кругового процесса. Работа в круговом
процессе равна балансу тепла (по первому началу термодинамики): ![]() . На участках
. На участках ![]() ,
,
![]() тепло к рабочему веществу не
поступает. Тепло
тепло к рабочему веществу не
поступает. Тепло ![]() поступает в систему в
процессе
поступает в систему в
процессе ![]() , тепло
, тепло ![]() выводится
из системы в процессе
выводится
из системы в процессе ![]() .
.
 РЕШЕНИЕ.
На основании проведенного анализа можно сделать вывод, что количество тепла
РЕШЕНИЕ.
На основании проведенного анализа можно сделать вывод, что количество тепла ![]() , а
, а ![]() :
:
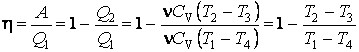 .
.
Запишем уравнения Пуассона для адиабат ![]() и
и
![]() соответственно:
соответственно:
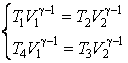 .
.
Делим почленно первое уравнение на второе:
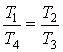 .
.
Преобразуем выражение для ![]() следующим
образом:
следующим
образом:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.