Способ повышения точности гирокомпасов класса «Sperry» MK-37VT

Глава 1. Способ повышения точности гирокомпасов класса «Sperry» MK-37VT.

1.1. Общие замечания.

В течение более полувека гироскопические компасы лидирующие в этой области стран (Германия, Соединенные Штаты Америки и Япония) обеспечивали приемлемую точность судовождения в соответствии с резолюциями ИМО №424 и 821. Надо особо подчеркнуть, что все гирокомпасы выпускаемые вышеперечисленными странами, относятся к классу некорректируемых (в отношении инерционной девиации, возникающей при маневрировании судна). Можно даже сказать, что величина указанной девиации в существеннейшей степени определяет класс важнейшего навигационного прибора, каковым является гирокомпас.

С появлением в середине 80-х годов XX века аналога корректируемого гирокомпаса класса «Вега», а позднее (к началу XXII) целой гаммы корректируемых гирокомпасов нового поколения с принципиально новым типом гироскопа ( динамически настраиваемый гироскоп) выявилось их большое преимущество (перед перечисленными выше зарубежными гирокомпасами) особенно в многократном повышении точности при маневрировании возможность обеспечения высокоширотного (вплоть до полюса) плавания.

Такое положение вещей заставило фирму (Аншютц) ФРГ искать радикальных путей повышения точности на маневрировании и тем самым некоторого расширения широтного диапазона использования гирокомпаса. В середине 90-х годов XX века фирма Аншютц создает гирокомпас «Standart-20», а вскоре вслед за ним еще более совершенный гирокомпас «Standart-22». Решение проблемы было найдено на основе включения в комплект гирокомпаса принципиального нового прибора- цифрового микропроцессора, в который заложена система дифференциальных уравнений третьего порядка. Вычисленные значения скоростной и инерционных девиаций дискретно подавать на коррекцию цифровых репитеров.

В результате точность гирокомпасов обеспечила выполнение требований ИМО при скоростях до 70 узлов и в диапазоне широт от 0-70 градусов. В работе [1] д.т.н., проф. Смирнов Е.Л. доказал ограниченность математической модели третьего и предложил математическую модель шестого порядка, которая обеспечивает большую точность гироскопов St-20 и St-22 в высоких широтах.

В самом начале XXI века США, следую за Германией создают цифровой гирокомпас Sperry MK37VT, также снабдив его микропроцессором в который заложена математическая модель гирокомпаса в виде линейной системы дифференциальных уравнений третьего порядка. Подчеркивая, что эта система была получена в СССР в 70-е годы XX столетия [2]. Принятая модель не является оптимальной в смысле точности. В данном разделе НИР предлагается и изучается другая математическая модель, на ряду с используемой в гирокомпасе Sperry МК-37VT.

1.2. Математические модели (системы дифференциальных уравнений) принятые для сравнительного анализа.

1.1

а) Система дифференциальных уравнений принятая в качестве математической модели в упомянутом выше американском гироскопе

б) предлагаемая, уточненная система дифференциальных уравнений для использования в качестве математической модели с целью повышения точности гирокомпаса Sperry MK37VT

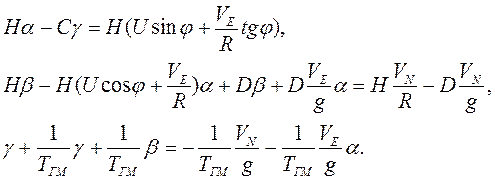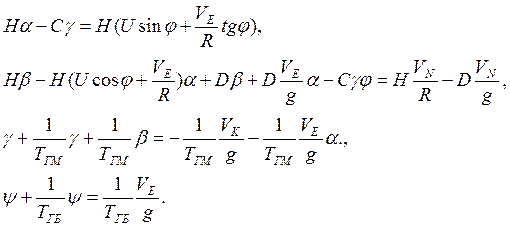1.2

Примечание. В системе (1.2) отчеркнуто дополнительное слагаемое во втором уравнении и новое (четвертое) уравнение. В приведенных системах уровнений использованы обычные обозначения:

Н - кинетический момент гироскопа

С – модуль момента гидравлического маятника

D – модуль момента демпфирующего маятника

Тдж – постоянная времени демпфирующей жидкости

Тгб – постоянная времени гироблока при его движении  в опорах подвеса упомянутого гироблока

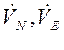–  ускорение объекта (соответственно северная и восточная составляющие при маневре объекта),

U – угловая скорость суточного вращения земли

VN, VE – соответственно северная и восточная составляющие движения объекта

j – широта места маневра

R – радиус земли, принятой за шар

 

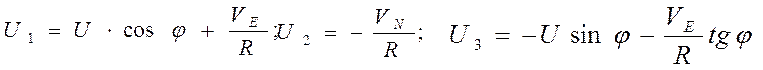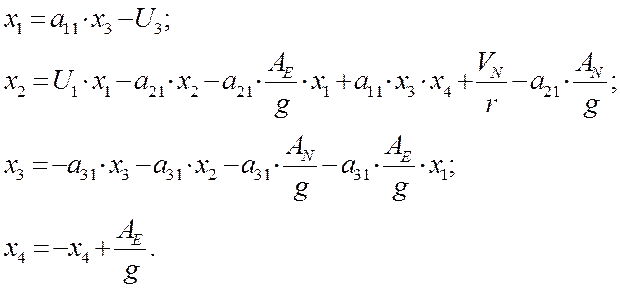
1.3

(1.3)–система предложенных дифференциальных уравнений, записанная в форме Коши. При интегрировании системы (1.3) результаты этой системы считаются эталонными.

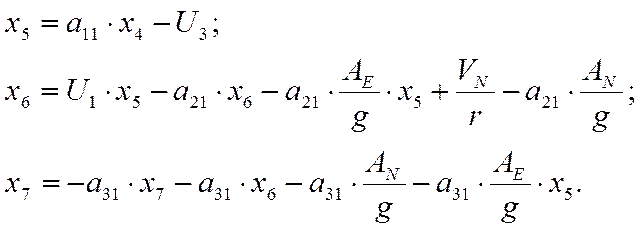
1.4

Система дифференциальных уравнений (1.4) используется как математическая модель в гирокомпасе Sperry MK37VT.

Числовое интегрирование систем (1.3) и (1.4) производилось методом Рунге – Кутта – Меерсона.

Из физических соображений вытекает, что никакого отличия системы (1.3) и (1.4) при маневрировании судна вдоль меридиана не может иметь место. Различие может быть только на четвертных румбах: 45⁰, 135⁰, 225⁰, 315⁰. Нет необходимости выполнять много численных примеров на всех четвертных румбах в силу идентичности результатов. По этой причине основной объем вычислений выполнялся для КК=45⁰. При этом вариации подлежат: широта места маневра, скорость маневра, длительность маневра. При вычислениях использовались следующие численные значения параметров гирокомпаса «Sperry MK37VT»:

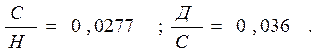
Результаты представлены в таблицах № 1 – № 26.

Таблица №1

V=70        tm= 30         fi=80        KK=45