Основные закономерности движения искусственного спутника Земли

2.1

2.  ОСНОВНЫЕ  ЗАКОНОМЕРНОСТИ  ДВИЖЕНИЯ  ИСЗ

Вычисление (в судовом  приемоиндикаторе  спутниковой  РНС)  координат  спутника на  орбите для каждого момента  времени является необходимым  условием расчета  координат  судна  по результатам  измерений  радионавигационных параметров.

2.1. Для понимания алгоритма расчета координат ИСЗ,  используемого в СРНС GPS, рассмотрим элементы эллиптической орбиты на плоскости

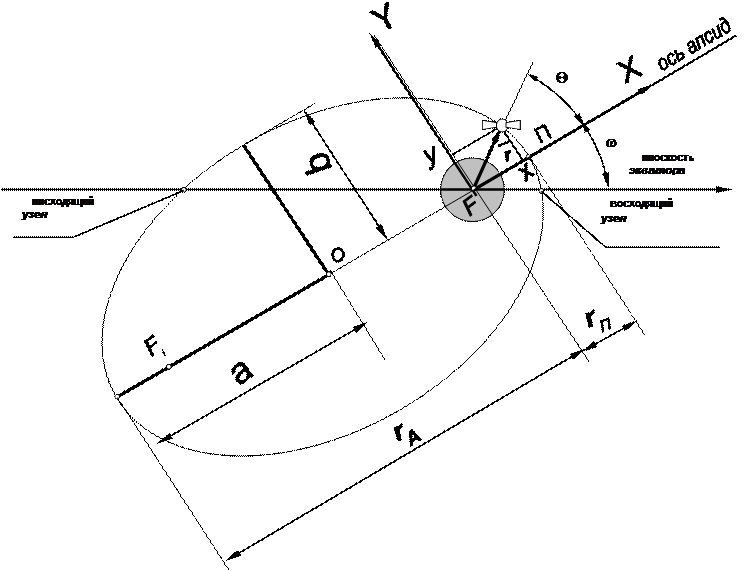
Траектория  движения ИСЗ иллюстрируется рис. 2.1.   Фокус  F  эллипса совмещен

с центром Земли.  Минимальное  и  максимальное  удаления ИСЗ от фокуса  называются соответственно  перигеем  (П)  и  апогеем (А).

В перигейной  системе координат (с центром в точке  F  при совмещении полуосей  a   и  b  с  осями   X    и    Y)  координаты ИСЗ удовлетворяют известному  уравнению эллипса.

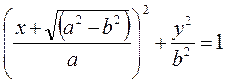
2.2.

Для задания  уравнения  эллипса в полярной  системе координат с центром в фокусе F   и полярной осью,  направленной на  перигей,  необходимо в предыдущее уравнение подставить 

             x = r Cosq,         y = r Sinq      ( 2.1 ),                                           

где  q -  угол  между  радиус-вектором и осью  апсид  (см.  рис. 2.1)  называется  истиннойаномалией.   Модуль  радиуса-вектора  ИСЗ  равен

                              ,

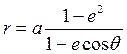где e- эксцентриситет эллипса, равный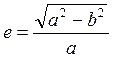  

Заметим,  что орбиты навигационных  ИСЗ  формируются с минимальным  возможным эксцентриситетом (около 1%),  исходя  из необходимости:

-  обеспечить одинаковые условия приема сигналов ИСЗ в любом наземном пункте;

-  уменьшить  разрядность величин  в  информации о параметрах орбиты, передаваемой  с  ИСЗ.  

         Координаты ИСЗ на  каждый  из  моментов  времени  t  могут быть рассчитаны,  если известны величины a, eи зависимость истинной аномалии  q   от времени  t.   Лишь для спутника с круговой орбитой   (эксцентриситет e= 0)   при известной величине  его периода  T  обращения вокруг Земли  эта  зависимость  элементарна:   q = 2p(t - t_п)¤T = M.   То есть в этом случае  истинная  аномалия  равна средней аномалии M.

Связь между средней аномалией M  и истинной аномалией  q   для эллиптической орбиты  может  быть  установлена,   если   найден период T обращения ИСЗ, который может быть рассчитан по формуле:

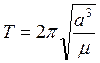                                         ( 2.2 ),

где   -  гравитационная постоянная Земли

2.2. Функциональная  зависимость  истинной  аномалии q  от  времени

дается соотношениями

                                          ,

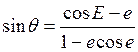
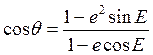где    -  эксцентрическая  аномалия,  величина которой на каждый момент времени  определяется  численным решением уравнения Кепплера

2.3.

Взаимосвязь  между эксцентрической и истинной аномалиями  показана на  рис. 2.2

	Рис.  2. 2.  Взаимосвязь истинной и эксцентрической аномалий

2.3.  Определение положения ИСЗ и  его орбиты в пространстве

2.3.1.  Понятия и обозначения элементов,  выбранных  для описания геометрического  положения  ИСЗ  в  спутниковых  РНС,  должны быть твердо усвоены. Это необходимо  для понимания  получаемых  соотношений и алгоритмов по расчету   координат и других  геометрических  параметров ИСЗ  и облегчит формирование  зримых представлений  о пространственном положении  спутников  относительно  Земли  и потребителей  в различных  типах   СРНС.

В  ряду используемых  систем  координат две  основные  -  декартовы  (инерциальная  и гринвичская)  имеют начало  в  центре  Земли  с  общей  осью  аппликат  -   осью  вращения  Земли.   Осьвращения  Земли  пересекает небесную  сферу в  полюсе мира. С  этой  осью  совмещены  оси     Z_и  и   Z       (см.  рис. 2.3) данных  систем координат.  Их плоскости  X_иOY_и  и    XOY  совмещены с экваториальной плоскостью  Земли.  Ось  абсцисс  X_иинерциальной  (неподвижной) системы  координат  направлена  на  созвездие Овна и параллельна  прямой,  соединяющей центры  Земли  и Солнца в момент весеннего  равноденствия (равной освещенности  Северного и  Южного полюсов  Земли).  Оси  X, Y гринвичской системы  вращаются вместе с Землей.  В  момент  равноденствия и далее  через  каждые  сутки  оси абсцисс  X_и  и  X оказываются  совмещенными.  

В  судовождении используются   координаты  наблюдателя (географические) с широтой  j_н и   долготой   λ_н.

2.4.

Некоторые геометрические  свойства СРНС  более наглядны  при  использовании  горизонтной  системы  координат,  в    которой ось Y обычно  совмещается  с  линией меридиана  и  направлена  на  Юг,  а ось  X - на  Восток (см.  рис. 2.4).    Положение  ИСЗ  в этом случае   задается    углом    n   кульминации   (возвышения)   и  углом     a.

Иногда   ось  горизонтной системы  задается по маршруту  движения судна -  выбор  координатной  системы обусловлен  удобством   пользователя.

 Эллиптическая орбита спутника, движущегося без возмущающих воздействий,    в  гринвичской  системе  координат   на  момент ее  совмещения  с инерциальной  приведена на   рис. 2.5   Ее основные    параметрами  являются:

-  долгота  W  восходящего  узла  -  точки    в которой плоскость  орбиты пересекается с плоскостью экватора при восхождении  спутника к точке перигея;

-  угол i  наклонения  орбиты,  т. е.  угол  между плоскостью орбиты  и плоскостью  экваатора;

-   угол перигея  w   (между  осью  OP перигея   и  линией      в плоскости  экватора,  соединяющей  центр  координатной  системы  с  восходящим узлом).