Определители. Матрицы. Действия над матрицами. Метод Гаусса, однородные системы уравнений

Определителем n-го порядка называется число, определяемое таблицей:

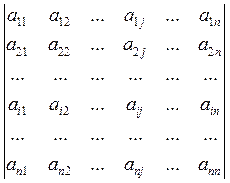
Минором М_ij элемента а_ij определителя n-го порядка называется определитель (n – 1)-го порядка, полученный из исходного путем вычеркивания i –ой строки и j –го столбца.

Алгебраическим дополнением А_ij элемента а_ij определителя n-го порядка называется минор, взятый со знаком ( – 1)^i+j.  т.е. А_ij = ( – 1)^i+j· M_ij

Теорема Лапласа: определитель n-го порядка равен сумме произведений элементов какого-либо ряда определителя на их алгебраические дополнения:

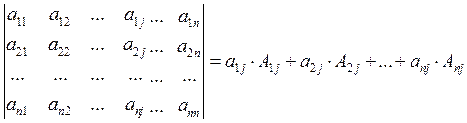 - разложение определителя по j-ому столбцу.

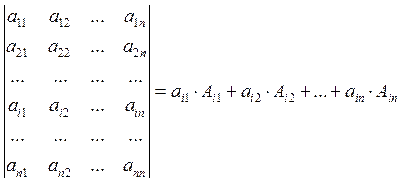  - разложение определителя по i –ой строке.

Свойства определителей:

1)  Если определитель имеет ряд, состоящий из одних нулей, то такой определитель равен нулю.

Например,  .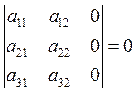

2)  Если определитель имеет пропорциональные ряды, то определитель равен нулю.

Например,  .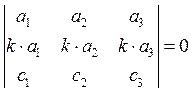

3)  Если поменять местами два каких-либо ряда определителя, то знак определителя изменится на противоположный.

Например,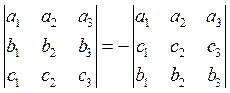 

4)  Если элементы какого-либо ряда определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

Например,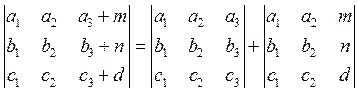 

5)  Определитель не изменится, если к элементам какого-либо ряда прибавить элементы другого ряда, умноженные на одно и то же число.

Например,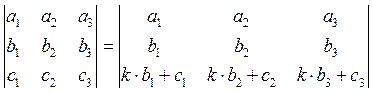 

6)  При транспонировании значение определителя не меняется.

Например,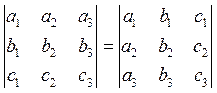 

7)  Теорема аннулирования: сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

Например: .

8)  Определитель треугольного вида равен произведению элементов главной диагонали:

Например:     .

Матрицы. Действия над матрицами.

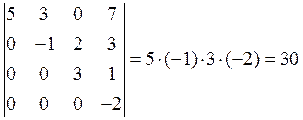Матрицей размерности mxnназывается таблица чисел, содержащая m строк и n столбцов: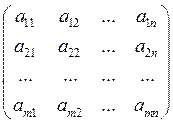

Если m = n, то матрица называется квадратной.

Числа а_ij называются элементами матрицы, индекс i - номер строки, j – номер столбца.

Квадратная матрица, у которой все элементы кроме диагональных равны нулю, называется диагональной.

Диагональная матрица, у которой диагональные элементы равны 1, называется единичной. Ее обозначают Е.

Например, .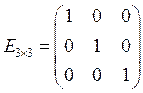

Над матрицами можно выполнять действия сложения, умножения на число, умножение матриц.

1. Сложение матриц определено только над матрицами одинаковой размерности.

Суммой 2-х матриц размерности mxn называется матрица mxn , каждый элемент которой равен сумме соответствующих элементов матриц. Т.е. А+B = C,  c_ij=a_ij+b_ij,  i =1..m, j=1..n.

2. Чтобы умножить матрицу на число, надо это число умножить на каждый элемент матрицы

λ·А = В,  b_ij= λ·a_{ij ,} i=1..m, j=1..n.

3. Умножение 2-х матриц определено в том случае, когда количество столбцов 1-ой матрицы равно количеству строк 2-ой матрицы.

Произведением 2-х матриц называется матрица, каждый элемент которой равен сумме произведений элементов i-ой строки первой матрицы на соответствующие элементы j-го столбца второй матрицы:

  A    ·    B    =     C,      c_ij=a_i1·b_1j + a_i2·b_2j +…+ a_im·b_mj   ,  i = 1…m,  j = 1…k          

mxnnxkmxk

Свойства действий над матрицами.

Квадратная матрица называется невырожденной, если определитель матрицы не равен нулю (detA ¹ 0), в противном случае матрица называется вырожденной.

Матрица А^-1 называется обратной для квадратной матрицы А, если А^-1 ∙ А = А ∙ А^-1 = Е.

Теорема существования обратной матрицы: всякая невырожденная матрица имеет обратную.

Обратная матрица для данной невырожденной матрицы вычисляется