Производная, правила дифференцирования, теоремы о среднем. Логарифмическое дифференцирование. Возрастание и убывание функции, экстремум функции

внутренняя точка, в которой касательная параллельна оси Ох.

Если, в частности,  f′(a) = f′(b) = 0, то теорема Ролля означает, что между двумя корнями функции содержится хотя бы один корень ее производной.

Теорема Лагранжа. Если функция f(x) непрерывна на отрезке [a; b], дифференцируема в интервале (a; b), то в этом интервале (a; b) найдется хотя бы одно значение х = с, при котором выполняется равенство:  

Геометрический смысл этой теоремы: на дуге АВ непрерывной кривой y = f(x), имеющей в каждой внутренней точке определенную касательную (не параллельную оси Оу), найдется хотя бы одна внутренняя точка, в которой касательная параллельна хорде АВ.

Теорема Коши. Если функции f(x) и g(x) непрерывны на отрезке [a; b] и дифференцируемы в интервале (a; b), причем g'(x) ≠ 0, то в этом интервале найдется хотя бы одно значение х = с, при котором 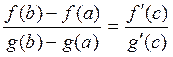, где a< с < b.

Производная сложной функции

Пусть y = f(u), u = u(x), тогда сложная функция имеет производную, равную , (т.е. производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной).

Производная обратной функции

Пусть у = f(х) и х = j(у) – взаимно обратные функции. Тогда, если функция у = f(х) имеет не равную нулю производную f ¢(х), то обратная функция имеет производную j¢(у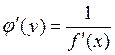) и  или, .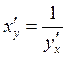

Таблица производных основных элементарных функций:

производные гиперболических функций. 

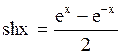  - гиперболический синус

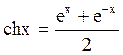 - гиперболический косинус (цепная линия)

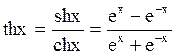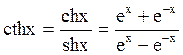  и    - гиперболический тангенс и котангенс (e – неперово число).

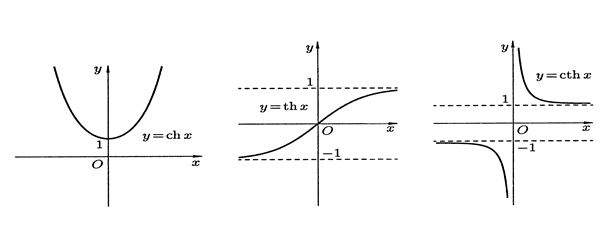
Свойства гиперболических функций:

1)  ch²x – sh²x = 1;

2)  sh(x ± y) = shx·chy ± chx·shy;

3)  ch(x ± y) = chx·chy ± shx·shy;

4)  ;

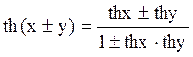5)  sh2x = 2·shx·chx;

6)   ch2x = ch²x + sh²x.

Производные гиперболических функций:

(shx)′ = chx ;   (chx)′ = shx ;  (thx)′ =  ;   (cthx)′ = .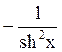

дифференциал функции.

Дифференциалом первого порядка функции y= f(x) в точке х называется главная часть приращения функции, равная произведению производной функции на приращение аргумента:  dy = f ¢(x)×Dx.

Дифференциал функции вычисляется по формуле:  .

Геометрический смысл дифференциала: дифференциал функции в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получает приращение Dx.

Инвариантная форма дифференциала 1-го порядка:  , где y(u) – сложная функция.

Применение дифференциала для приближенных вычислений

Задача 1: Найти дифференциал функции

Дифференциал функции находится по формуле:

Найдем производную: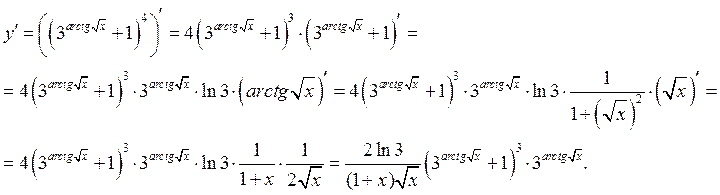

    Тогда дифференциал функции: .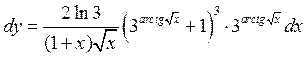

Задача 2: Вычислить приближенно с помощью дифференциалов arctg1,02.

Выбираем х₀ = 1, т.к. эта точка ближайшая для 1,02 и значение функции в ней можно вычислить точно: f(x₀) = arctg1 = .

Тогда x₀ + Δx = 1,02 ÞΔx = 1,02 - 1 = 0,02

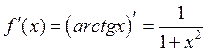 Þ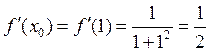

Подставляем в формулу: f (x₀ + Δx) ≈ f (x₀) + f ¢ (x₀) ∙ Δx

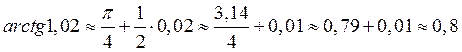
производная неявно заданной функции.

Под неявным заданием функциипонимают задание функции в виде F(x,y) = 0 не разрешенного относительно у.

Для нахождения производной неявно заданной функции нужно продифференцировать это уравнение по х, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у′. Производная неявно заданной функции выражается через х и функцию у.

Задача 3: Найти производную функции .

Функция задана неявно, т.к. задана уравнением неразрешенным относительно у.

Дифференцируем обе части уравнения:

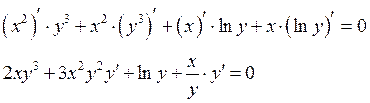
Выражаем у':

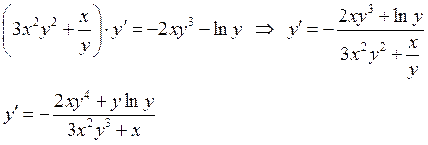
логарифмическое дифференцирование.

Функция вида y = u^v , где u и v – функции от х, называется степенно-показательной функцией.

Для нахождения производной степенно-показательной функции используется метод логарифмического дифференцирования.

Логарифмическое дифференцирование

1) прологарифмируем обе части уравнения функции:   

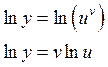
2) дифференцируем обе части:   

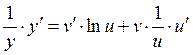
3) отсюда находим производную у′ :

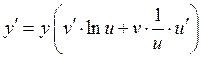, т.е. .

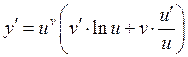производные и дифференциалы высших порядков.

Производной n-го порядка от функции  называется производная от производной (n–1)-го порядка .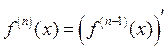

Дифференциалом n-го порядка функции  называется дифференциал от дифференциала  (n-1)-го порядка  , т.е.

Формула Лейбница

Производные высших порядков неявно заданных функций

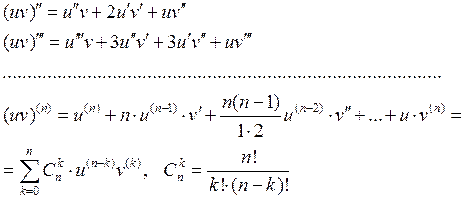
Для того чтобы найти производную функции нужно продифференцировать обе части уравнения F(x; y) = 0 и выразить у'. Затем дифференцируем по х первую производную и выразим . Подставив найденное значение у' в выражение второй производной, выразим  через х и у.

Аналогично поступаем для нахождения производной 3-го порядка