Определение угловой пространственной ориентации судна в сетевой спутниковой радионавигационной системе

ОПРЕДЕЛЕНИЕ УГЛОВОЙ ПРОСТРАНСТВЕННОЙ

ОРИЕНТАЦИИ  СУДНА  В  ССРНС

5.1.  Принцип определения углового положения

         короткого  отрезка  прямой  в  ССРНС

            Как  известно  из аналитической  геометрии и векторной  алгебры, угловое положение отрезка прямой линии (например,  между точками  0 и 1 на  рис. 5.1 –  вектора a)  в  декартовой системе координат  однозначно определяется  величинами его проекций   a_x,  a_y,  a_z  на оси  OX_г,  OY_г,  OZ_г   горизонтной  системы координат.   Покажем,  как  величины данных проекций могут быть определены  в среднеорбитальной  СРНС.

  Полагаем, что судовая приемная  антенна ССРНС  установлена  в точке   O   - центре горизонтной системы координат (там же и точка 0 -  начало вектора  a).  При  одновременном  слежении  за   k  спутниками могут быть   определены координаты  точки  O  и,  следовательно,  (при  известных координатах i-го  спутника)  рассчитаны    его  проекции  x_i,  y_i,  z_i    на  кординатные  оси. 

Воспользуемся  выражением  для скалярного произведения  векторов (там же и точка 0 -  начало вектора  a  и r_i,  которое  равно:

                   a × r_i   =  x_i a_{x +}  y_i a _{y +}  z_i a_z   =   | a | × | r_i |   cos q_i                    ( 5.1 )

Разделив  (5.1)  на  | R_i |,  получим

                              c_xi a_{x +}  c_yi a _{y +}  c_zi a_z   =   | a |  cos q_i                               ( 5.2 )

Величину   скалярного  произведения | a | cosq_i  получим, определяя  разность  расстояний  | R_i,0 |  и  | R_i,1|     между  i-м  спутником  и  точками  0   и  1.

Из   рис. 5.1  очевидно,  что квадраты  указанных  расстояний  соответственно равны:

                (r_i,0)²  =  x_i ²₊  y_i ² ₊  z_i ²;

                 (r_i,1)²  =  (x_i - a_x) ²₊  (y_i – a_y) ² ₊  (z_i – a_z) ²  =

                            =   x_i²₊  y_i² ₊  z_i²    - 2x_i a_x    - 2y_i a_y    - 2z_i a_{z      +}  a_x²₊  a_y² ₊  a_z ²;

При этом    разность квадратов указанных  расстояний  будет равна

(r_i,0  -   r_i,1)²  =    (r_i,0     -  r_i,1)  (r_i,0   +   r_i,1)  = 

                       =   2x_i a_x    + 2y_i a_y    +  2z_i a_z       -  a_x²  -  a_y² -  a_z ².

Разделим  полученное равенство  на   (r_i,0   +   r_i,1), учитывая ,  что  в  ССРНС при     r_i,0  >2 × 10⁷ м     и   | a |,  не  превышающем  единиц  метров, можно  с высокой точностью  полагать,  что      r_i,0   +   r_i,1  @  2 r_i,0 ,    а  величины   a_x²,  a_y²,  a_z ²   пренебрежительно малы  относительно    величин   2x_i a_x ,  2y_i a_y ,  2z_i a_z.  После простейших  преобразований  получим   уравнение

                                                 c_xi a_{x +}  c_yi a _{y +}  c_zi a_z    @   r_i,0     -  r_i,1 ,                                    ( 5.2 )

где   a_x ,   a _y ,  a_z  - искомые и  неизвестные   величины,

        r_i,0    -  r_i,1     - разность  расстояний,  которая может быть определена по результатам измерений  (в том  числе  и фазовых)  разности времени  между моментами  прихода сигнала  от  ИСЗ  в  точки  0  и  1.

Очевидно,  что определение  трех  неизвестных  возможно при  составлении и решении системы  из  3-х  или  более  уравнений   с  3-мя  неизвестными. То есть,  разности  расстояний   r_i,0     -  r_i,1   должны  определяться,  как минимум,  до  трех   ИСЗ.

5.2.  Схема  измерений  для определения  разности расстояний

между  ИСЗ,  началом   и  концом  отрезка  прямой

Определение  разностей  расстояний     r_i,0   -  r_i,1  может быть  осуществлено  при  использовании  схемы,  представленной на рис. 5.2    и  содержащей  приемные антенны  0  и  1 (установлены  соответственно в точках  0 и 1  рис. 5.1),   подключенные  к ним приемники  ПК0  и  ПК1   и  фазометр ФМ 0-1.

Полагая,  что   с  ИСЗ   излучаются  незатухающие колбания  вида

E_с   =  E_m   Sin  (2pf_сt    +   j_с),

в точках  приема  0   и   1  базовой линии   a  получим колебания

                            E₀   =   E_{m п}  Sin  (2pf_с (t  -  r₀  / c)    +   j_с),

                            E₁   =   E_{m п}  Sin  (2pf_с (t   -  r₁ / c)    +   j_с).

           Колебания   на  выходах приемников соответственно  ПК-0  и  ПК-1  можем записать в виде

                                  U₀   =   U_m Sin  (2pf_с (t  -  r₀  / c)    +   j_с      +   Dj₀),

                                  U₁   =   U_m  Sin  (2pf_с (t   -  r₁ / c)   +   j_с     +  D j₁ ),

где   Dj₀     и   Dj₁   -  фазовые  сдвиги  колебаний,  появляющиеся у сигналов после прохождения через приемоизмерительные  цепи .

                  Разность  фаз,    измеренная  фазометром    ФМ 0-1, будет  равна

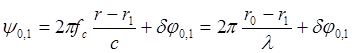                                                ,       ( 5.4 )