Определение угловой пространственной ориентации судна в сетевой спутниковой радионавигационной системе, страница 3

     5.3.2. На практике используются и другие методы и параметры описания угловой ориентации. В «автопилотах» - устройствах автоматичемкого управления движением изменение ориентации производится /13/ путем последовательного поворота корпуса относительно ортогональных осей подвижной системы  на  углы :

«и» -  поворота вокруг судовой оси аппликат,

«д» - поворота вокруг поперечной оси судна (оси ординат),

«к» -  поворота вокруг продольной оси судна (оси абсцисс).

Эти углы Эйлера (и, к, д) обозначены здесь строчными буквами для указания на их качественное и количественное  отличие  от принятых выше {И,  К, Д}. Одной и той же угловой ориентации с углами {И,К,Д} соответствует более дюжины представлений этой же угловой ориентации  с помощью различающихся триад углов Эйлера [и,к,д] в зависимости от порядка используемых двух или трех осей вращения. 

В  отдельных  случаях   могут иметь  место  равенства  указанных  параметров.    Так  на рис. 5.4,  построенном при повороте плоскости X_c О_с Y_c    первоначально  на угол  и   вокруг  совмещенных  осей  O_гZ_г     и     O _с Z _с,   затем  на угол  д  вокруг  оси О_с Y_c   (поперечной)  и, наконец,  на  угол  к  вокруг   оси О_с X_c,    показано ,   что   И=и,  а   Д=д,   но  К¹к.

Для математического описания  ориентации можно применить алгебру кватернионов, возможны и другие методы, кратко освещаемые в разделе14.10 из /13/.   Однако при первом знакомстве с задачей угловой ориентации достаточно ограничиться определением однозначных параметров И, Д, К с учетом того, что однозначная и полная информация об  угловой пространственной ориентации  судна содержится лишь в значениях направляющих косинусов углов между  осями симметрии судна и осями принятой неподвижной (например, горизонтной) системы координат.

5.3.3. Средние квадратические погрешности определения  направляющих косинусов при одинаковых СКП  s_c величин c_ai и c_bi  нормированных по (5.5) разностей расстояний (5.4)  выражаются аналогично (3.6):

;                                (5.8)

.                                          (5.9)    

Связь погрешности истинного курса  DИ (в радианах) с  погрешностями  направляющих  косинусов можно  выразить ,  полагая,  что величина  погрешности  DИ (в радианах)  может быть представлена  выражением

.

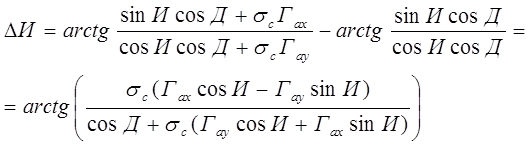Учитывая,  что  при реальных  величинах  дифферента   Д£20°  величина ,  а   ,  величина  погрешности  DИ (в радианах)  может быть представлена  выражением

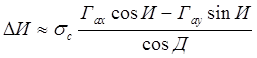                                                    .             ( 5.10 )

Погрешность  найдем,  учитывая,  что                       

при    Д£20°по  данным  выше  соображениямможет  быть  представлено в виде

                                     ,

откуда 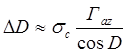                                                                 .                        ( 5.11 )

Аналогично 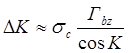                                                         .                        ( 5.12 )

При фазовых измерениях - из-за небольшого разноса антенн - влияние нешумовых источников погрешностей (перечисленных в п.1.3.2) не должно сказываться.  Влияние шумов можно оценить по полученному с помощью (1.13) и (1.15) соотношению для среднеквадратической погрешности s_cш нормированной величины с=Dr/ l из (5.5):

   s_cш»(0,0428/l)[П^ссн(N₀/Р)]^0,5(рад.)=(2,452/l)[П^ссн(N₀/Р)]^0,5(град.).             (5.13)

Оценим   возможную  погрешность  определения   направления,  учитывая, что  по результатам  исследований средняя квадратическая  погрешность фазовых  измерений  s_y =   0.015  × 2p.  При измерении разности фаз с погрешностью s_y выражение   (4.3.1)   можем  представить в виде:  

                                                                                 b_y

Dy_0,1    +  s_y   =2p   ×  ¾  × Cos (q   + s_q )                   

                                                                                l

Вычитая  из   него  величину  Dy_0,1 ,   получим

      b_y                                                                                   b_y

2p  ¾  [ Cos (q   + s_q ) -  Cos q ] = 2p ¾  [ 2 Sin(q   + s_q / 2 )   Sin (s_q / 2) ]  =  s_y .

l                                                        l

При  выражении величины s_q/ 2  в радианах из-за ее малости Sin(s_q / 2) @   s_q / 2.  .

Тогда  после  простых  и очевидных  преобразований   получим

                                                                           s_y            l          1

                                                         s_q    @¾¾  ×  ¾  ×  ¾ ¾¾  .

                                                                            2p        b        Sin q

В  случае   l =0,2 м,  b  = 1 м,   q   =   30°,  s_y  /  2p  =   0.015        получим   выраженную в  градусах   величину  погрешности  определяемого  РКУ,  равную   s_q=  0.34°.  При  увеличении  разноса  антенн   величина погрешности   s_q может  быть сведена  до  нескольких  угловых  минут.