Операторы физических частиц, страница 5

или

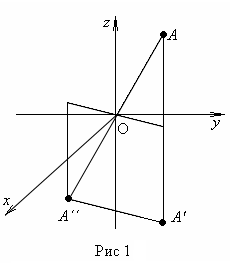
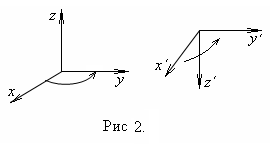
х´ = - х;   у´ = - у;   z´ = - z.

Операцию инверсии можно провести в два этапа, комбинируя отражение в зеркале и поворот на π. На рис.6.1. точка А при отражении в зеркале, поверхность которого совпадает с плоскостью хоу, переходит в точку А΄. Если совершить еще и поворот вокруг оси о_z, то точка А΄ совместиться с точкой А΄΄, координаты которой связаны с координатами точки А преобразованиями инверсии. Поэтому симметрия систем относительно инверсии непосредственно связана с симметрией относительно отражения в зеркале – с симметрией «правого» и «левого».

Всякое преобразование координат можно трактовать двояко: как следствие перемещения системы (при неизменных осях координат) и как следствие применения положений осей координат (при этом физическая система остается неподвижной), тогда правая декартова система координат переходит в левую (рис.6.2).

Предположим, что состояние физической системы не изменяется при инверсии. Пусть до преобразования она описывала волновой функцией Ψ(). Волновая функция f(), описывающая систему после преобразования, должна удовлетворять равенству:

.                                        (6.1)

Введем оператор, изменяющий вид функции при изменении знака у координат, и назовем его оператором инверсии:

.

Согласно (6.1) имеем:

.                                      (6.2)

Если оператор  коммутирует с гамильтонианом, то существует закон сохранения некоторой физической величины, которая называется четность.

Для определения допустимых значений четности запишем уравнения для собственных функций и собственных значений оператора инверсии:

.                                         (6.3)

Применяя оператор  к обеим частям соотношения (6.3), получим:

.                                       (6.4)

Но согласно определению оператора инверсии (6.2) последовательное применение его к любой функции дважды даст исходную функцию:

.                           (6.5)

Сравнивая уравнения (6.4) и (6.5), находим, что р² = 1, а р = ±1 – собственные значения оператора инверсии  -1 и +1.

Эти два числа и принимаются за значения новой физической величины – четности состояния микросистемы или системы микрочастиц.

Если функция состояния не изменяется при инверсии осей, то состояние четное, а четность равна +1; если изменяет знак – нечетное, четность  -1.

Если  и  коммутируют, то существуют состояния с определенной энергией и определенной четностью, т.е. состояния, в которых четность сохраняется.