Операторы физических частиц, страница 3

Оператор Гамильтона характеризует микросистему с динамической стороны, его вид зависит от масс частиц, их электрических зарядов, взаимодействия между ними. В принципе гамильтониан должен быть задан в конкретных задачах квантовой механики подобно тому, как задаются силы в классической механике при использовании второго закона Ньютона.

Волновые функции – решения уравнения Шредингера – являются комплексными функциями вещественных переменных. Аргументы волновой функции – координаты и время.

Состояние квантовой системы описывается волновой функцией, которая ничего не говорит о значениях физических величин, которыми характеризуются система. Такую информацию дает только измерение, результат которого не всегда однозначен. Получение того или иного значения на опыте в ряде случаев является случайным событием. Тогда говорят, что величина не имеет определенного значения. Однако можно рассчитать вероятность данного значения при многократных измерениях, располагая функцией состояния: вероятность того, что при измерении получится значение а_i физической величины А, равна квадрату модуля соответствующего коэффициента Фурье в разложении волновой функции в ряд или интеграл Фурье по собственным функциям оператора этой физической величины.

Пусть Ψ – волновая функция частицы, чтобы рассчитать искомые вероятности, представим ее в виде ряда:

,

где ψ_i – собственные функции оператора Â, имеющего дискретный спектр, тогда вероятность получения а_i есть:

.

В случае непрерывного спектра волновая функция разлагается в интеграл Фурье. Если ψ(а,х) – собственная функция, то:

.

Поскольку теперь мы имеем непрерывное множество значений величины А, то в строгом смысле слова нельзя говорить о вероятностях отдельных значений. Вероятность dΩ попадания значений величины в интервал от а до (а + da) равна:

dΩ(a) = ω(a)da,

где ω(а) – плотность вероятности (функция распределения вероятностей) равна квадрату модуля коэффициента с(а):

.

Ясно, что определенного значения у величины нет, если функция состояния не является собственной для оператора этой величины. В этом случае определяют среднее значение достаточно большого числа измерений:

.

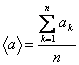Для теоретической оценки среднего значения физической величины достаточно знать функцию состояния частицы (предполагается, что вид оператора этой величины известен). Если а_i – собственные значения оператора Â и Ω_i – вероятности их обнаружения, то среднее значение:

.

Подставив Ω_i, имеем:

,

где Ψ – волновая функция,       ψ_i – собственные функции оператора Â(Âψ_i = а_iψ_i), тогда:

.

Вычисление средних имеет большое значение для микромира. Когда в рассматриваемом состоянии физическая величина не имеет определенного значения, среднее значение характеризует состояние.

Понятно, что если Ψ = ψ_i, то:

,

где ψ^* = 1.

В стационарном состоянии: .