 Министерство
образования Российской Федерации
Министерство
образования Российской Федерации
Рыбинская государственная авиационная технологическая академия имени П. А. Соловьева
Кафедра радиоэлектронных и телекоммуникационных систем
КИРИЛЛИН А. Н.
прохождение Радиоимпульсов через
избирательные цепи
Методические указания
к лабораторной работе по дисциплине
"Основы радиоэлектроники и связи"
Рыбинск
2003
Цель работы – исследование искажений, возникающих при прохождении радиоимпульсов с прямоугольной огибающей и гармоническим заполнением через последовательный, параллельный и связанные контуры.
5.1 Краткие теоретические сведения
Для нахождения отклика избирательной линейной цепи при действии на входе радиоимпульса с прямоугольной огибающей и гармоническим заполнением необходимо рассмотреть процессы на фронте (при включении гармонического колебания) и срезе импульса (при его выключении).
Для этого используют различные методы:
– классический (наложения свободных и вынужденных колебаний), позволяющий получить наглядную физическую интерпретацию результатов;
– приближенный спектральный, с помощью которого можно найти комплексную огибающую выходного колебания:
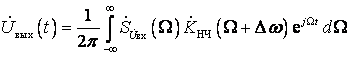 , (5.1)
, (5.1)
где
![]() – спектральная плотность комплексной
огибающей входного высокочастотного колебания;
– спектральная плотность комплексной
огибающей входного высокочастотного колебания;
![]() – комплексный коэффициент передачи
цепи, приведенный к текущей частоте
– комплексный коэффициент передачи
цепи, приведенный к текущей частоте ![]() ;
;
![]() – абсолютная расстройка;
– абсолютная расстройка;
![]() – несущая частота сигнала;
– несущая частота сигнала;
![]() – резонансная частота контура;
– резонансная частота контура;
– метод интеграла Дюамеля для огибающих, в соответствии с которым
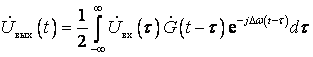 , (5.2)
, (5.2)
где ![]() – комплексная огибающая входного
сигнала;
– комплексная огибающая входного
сигнала;
![]() – комплексная огибающая импульсной
характеристики цепи.
– комплексная огибающая импульсной
характеристики цепи.
Анализ установления режима в последовательном
колебательном контуре при включении гармонического колебания ![]() приводит к следующим результатам для
тока в контуре:
приводит к следующим результатам для
тока в контуре:
–
при ![]()
![]() , (5.3)
, (5.3)
где ![]() – постоянная времени контура;
– постоянная времени контура;
![]() – добротность контура;
– добротность контура;
– при ![]()
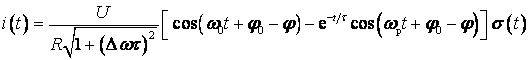 , (5.4)
, (5.4)
где ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.