Различия между 2-мя группами (использование условий отбора). Различия между 2-мя смежными выборками (и условия отбора). Корреляционная связь между 2-мя переменными (и условия отбора), страница 2

По какой зависимой переменной группы различаются более сильно? По какой зависимой переменной различия между группами менее выражены?  Отвечая на этот вопрос, учитывайте изменчивость оценок в каждой из групп. Обязательно сопоставляйте числовые деления вертикальных осей графиков. Например, на графиках различия между 2-мя группами по одной зависимой переменной могут выглядеть примерно также, как и различия между этими группами по другой зависимой переменной. Однако, после более внимательного рассмотрения может оказаться, что по одной зависимой переменной может быть оценки изменяются в диапозоне от 1 до 7, а по другой зависимой переменной – от 5 до 7.

Box-диаграммы еще нам пригодятся, сохраните их под именем box.stw.

sm 3.3. Статистическая значимость различий между 2-мя группами

Box-диаграммы являются наглядными, но Вы не можете использовать их для принятия решения об отклонении (либо о неотклонении) нулевой гипотезы . Чтобы принять это решение, Вы должны рассчитать эмпирический уровень статистической значимости p. Если этот уровень меньше критического значения 0,01 (или 0,05), то Вы можете отклонять нулевую гипотезу .

Вычисления и анализ

Итак, сейчас Вы должны проверить статистическую значимость различий между 2-мя группами по 2-м зависимым переменным. Для решения подобных задач, в зависимости от ситуации, используется либо U-критерий Манна–Уитни, либо t-критерий Стьюдента. Если зависимые переменные не являются метрическими, то применение t-критерия Стьюдента считается некорректным. Но в учебных целях мы сейчас временно проигнорируем эту проблему. Ведь сейчас мы в большей степени изучаем не условия применения метода, а процедуру его вычисления.

Прочитайте начало инструкций “s2”. Вычислите t-критерий Стьюдента, пользуясь инструкциями s2.2. Сформулируйте нулевую гипотезу . По какой зависимой переменной Вы можете отклонить ? На каком уровне (p≤0,01 или p≤0,05) можно считать статистически значимыми различия по этой зависимой переменной? Найдите построенные ранее Box-диаграммы (файл Box.stw) и убедитесь, что информация, предоставляемая Box-диаграммами, соответствует информации о статистической значимости различий.

Вычислите U-критерий Манна-Уитни, пользуясь инструкциями s2.1. Какую величину уровня значимости (p-level) Вы получили для каждой зависимой переменной? Позволил ли U‑критерий выявить статистически значимые различия хотя бы по одной зависимой переменной? Если да, то по какой переменной и на каком уровне? Если же статистически значимых различий согласно U-критерию нет, то сейчас это можно объяснить малым объемом выборки и малой мощностью непараметрических критериев.

Отключение условия отбора

Если в ваших дальнейших исследованиях исходные данные будут иметь более простую структуру, то условие отбора Вы использовать не будете. Поэтому надо, чтобы включение и отключение условия отбора не было для вас сложным. Закройте все окна кроме вашего файла *.sta и отключите условие отбора.

sm 4. Различия между 2-мя смежными выборками (и условия отбора)

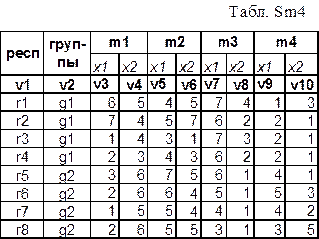Просмотрите исходные данные в табл.Sm4. Несколько респондентов (их обозначения содержатся в переменной v1), распределенные по 2-м группам (обозначения групп содержатся в переменной v2), оценивали четыре явления по нескольким характеристикам (х1, х2, …) в 7-балльной шкале. Для оценивания каждого из явлений использовался один и тот же набор характеристик. Последовательность оценивания явлений соответствует их номерам: вначале оценивалось явление m1…, в последнюю очередь оценивалось явление m4.

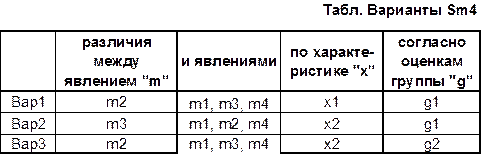Введите в таблицу *.sta программы STATISTICA все данные о группах, т.е. один столбец, состоящий из 8 строк. Просмотрите в таблице «Варианты Sm4» обозначение характеристики «х», по которой Вам необходимо проверить различия в соответствии с вашим вариантом? Добавьте в таблицу *.sta оценки всех 4-х явлений по этой характеристике. В итоге все ваши исходные данные в таблице *.sta должны занимать 8 строк и 5 столбцов. Кстати, все эти данные уже содержатся в файле Sm4.sta. Но, даже если Вы найдете этот файл, проверьте его на соответствие с табл.Sm4, поскольку его могли изменить другие пользователи.