Тензором напряжений описывается напряженное состояние в точке. При выборе определенной ориентации осей xٰ, yٰ, zٰ можно получить tij=0, при этом получаем тензор главных напряжений:
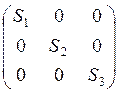Аналитическая
форма
Геометрическая форма
Круги Мора
В зависимости от внешних нагрузок матрицы будут разные. Нормальные напряжения приводят к образованию трещин: чем больше доля нормального напряжения, тем выше вероятность образования и развития трещины. Касательные напряжения влияют на пластическую деформацию.
Напряженное состояние рассчитывается с целью найти точку, в которой вероятнее всего произойдет разрушение детали. Это опасное место будет характеризоваться максимальной долей нормальных напряжений.
Главный тензор напряжений упрощается переходом к α – коэффициент мягкости напряженного состояния.
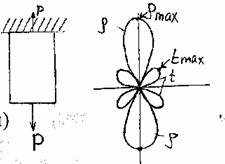
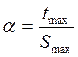
при растяжении α=0,5
при кручении α=0,8
при вдавливании α=2
при всестороннем сжатии α=4
при всестороннем нагреве α=0,004
т. е вероятность разрушения минимальна при всестороннем сжатии, т.к. в этом варианте нормальное напряжение минимально.
Для пластической деформации металлов наиболее часто
используется прокатка, так как при ней коэффициент мягкости напряженного
состояния стремится к 4.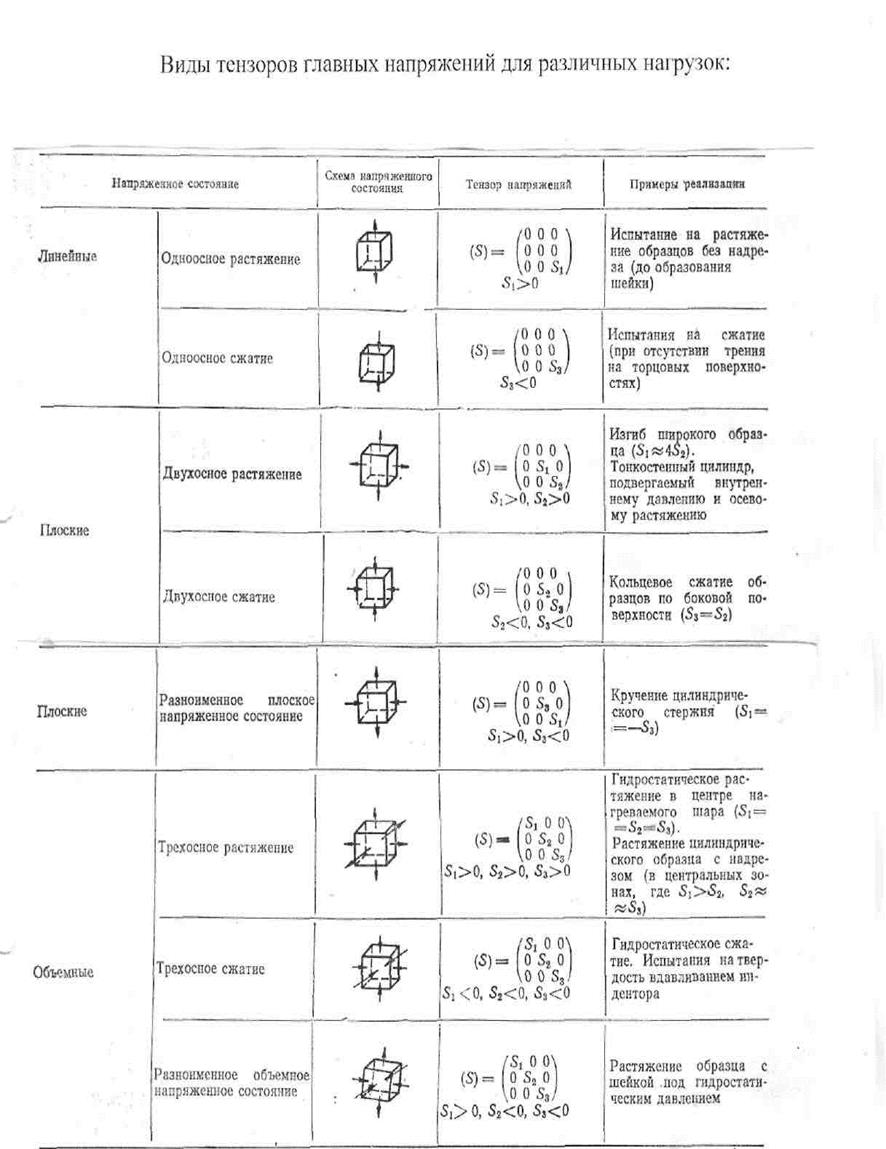 
МОДЕЛЬ ОТКЛИКА НА МЕХАНИЧЕСКОЕ ВОЗДЕЙСТВИЕ.
ДЕФОРМАЦИЯ.
Деформированное состояние – объемное распределение удлинений и сдвигов точки детали, вызванных напряженным состоянием, действующим в этой точке.
Напряженное состояние описывается нормальным напряжением S, которое вызывает удлинение e, и касательным напряжением t, которое вызывает сдвиг g.
Истинное относительное удлинение рассчитывается по формуле
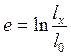
Удлинение и укорочение образца обычно происходит под действием нормальных сил. Касательные напряжения вызывают сдвиговые деформации, которые оцениваются по углу сдвига α (в радианах) или по величине относительного сдвига g= tg α
Совокупность удлинений и сдвигов – тензор деформации – по аналогии с тензором напряжений характеризует любое деформированное состояние в данной точке и позволяет определять е в любом направлении и g в любой плоскости.
Тензор главных напряжений. Можно выбрать такие оси xٰٰٰ ٰ , yٰ ٰ , zٰ ٰ в которых тензор имеет вид
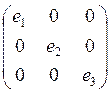
где е1 и е3 – наибольшее и наименьшее удлинение.
Напряженное состояние вызывает деформированное состояние. В общем случае тензор деформаций характеризуется девятью компонентами – тремя удлинениями и шестью сдвигами:
Механическое свойство
|
Напряженное состояние |
Механические свойства |
Деформированное состояние |
= *
Механическое свойство – характеристика реакции материала на внешнее воздействие; характеристика деформации материала возникающей в результате внешнего воздействия. Оно проявляется в виде упругости, пластичности, разрушения.
Деформации
Упругая деформация – деформация, исчезающая после снятия нагрузки.
, где 
- модуль упругости,
= x,y,z –
любые.
Растяжение стержня 
- закон
Гука
В случае пластической деформации аналитическая зависимость усложняется, поэтому пластические свойства описываются графически, как и разрушение.
Данный подход действителен только при равномерном распределении нагруженного состояния. Напряженное состояние в точке зависит от:
1. характера распределения макро сил;
2. формы нагруженного тела;
3. распределения дефектов структуры нагруженного тела.
ДВЕ ФОРМЫ ОТОБРАЖЕНИЯ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЙ
Истинная форма записи
|
Напряженное состояние |
Деформированное состояние |
|
|
|
Обязательное условие деформации – неизменность объема.
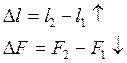
Условная запись (сечение не меняется)
|
Напряженное состояние |
Деформированное состояние |
|
|
|
Коэффициент Пуассона
,
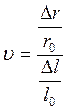для металлов 
Например
=25% 
e=ln1,25=22%
= 100% e=ln2=69%
Чем меньше степень деформации, тем меньше расхождение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
