Вязкому разрушению предшествует пластическая деформация, поэтому оно всегда идет с большей затратой энергии на разрушение.
Влияние температуры на процесс разрушения материалов с ОЦК кристаллической решеткой (α-Fe, Mo, Cr, V, W).
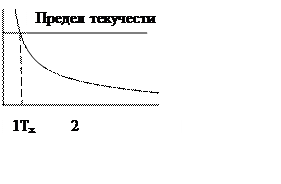Схема Иоффе
скол (отрыв) не зависит от температуры
1 – область хрупкого разрушения
2 – область вязкого разрушения
Тх – температура хладноломкости
Переход к хрупкому разрушению при понижении температуры происходит в соответствии со схемой, предложенной в работах А.Ф. Иоффе. Он предполагает, что предел текучести и разрушающее напряжение не связаны друг с другом, при этом предел текучести в значительно большей степени зависти от температуры, чем разрушающее напряжение. Существует температура Тх, при которой кривые предела текучести и напряжения разрушения пересекаются. Выше Тх металл разрушается пластично, поскольку увеличивающееся напряжение сначала достигает значения, соответствующего пределу текучести. Ниже Тх наблюдается хрупкое разрушение, т.к. растягивающее напряжение раньше достигает критической величины, равной разрушающему напряжению. Хрупкое разрушение, таким образом, связано с резким увеличением предела текучести при понижении температуры. Температура Тх является температурой перехода от пластического состояния к хрупкому и ее называют также порогом хладноломкости.
На распространение трещин влияет:
1.Неравномерность материала, а именно неметаллические включения (MnO, MnS, MnP, Fe3C, Cr3C6)
2. Волокнистость – это химическая неоднородность, которая остается при прокатке. Вдоль волокна трещине распространяться значительно легче, чем поперек волокна.
6.Макроскопический уровень.
Параллельно с разработкой физических представлений о процессах разрушения развивалась механика разрушения – наука, занимающаяся комплексом вопросов, связанных с анализом условий катастрофического хрупкого разрушения. Механика разрушения возникла на базе теории Гриффитса, модифицированной с учетом неизбежного участия пластической деформации в процессе разрушения металлов. Особенно резкий толчок развитию механики разрушения дали участившиеся в годы второй мировой войны и послевоенное время случаи аварийных разрушений крупных конструкций – корпусов кораблей и ракет, сосудов давления, мостов, и т.д. Впечатляющий перечень аварий и катастроф, связанных с внезапным хрупким разрушением конструкций, не оставляет сомнений в насущной необходимости разработки научных методов расчета конструкций для предотвращения такого рода разрушений.
По существу для конструкторов совершенно необходимо знание сопротивления материала распространению хрупкой трещины, чтобы установить связь между допустимым напряжением и размером трещины или трещиноподобного дефекта, который может с самого начала присутствовать в конструкции. Механика разрушения призвана дать обоснованную методику лабораторных испытаний, результаты которых можно было бы переносить на проектируемые изделия.
Механика разрушения прибавила к портрету трещины еще одну величину – критическую длину трещины. До критической длины наблюдается медленный рост трещины, и происходит вязкое разрушение, а после критической длины трещина быстро распространяется, протекает хрупкое разрушение материала.
При хрупком разрушении скорость распространения трещины достигает 0,4-0,5 скорости распространения звука в материале образца, а в случае вязкого разрушения трещина распространяется со скоростью, соизмеримой со скоростью деформации образца.
Механикой разрушения было введено понятие критическая длинна lкр.. До lкр трещина растет медленно, после преодоления lкр – очень быстро и хрупко.
Формула Гриффица
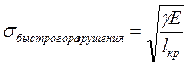
- формула напряженного быстрого разрушения для стекла, g - работа по образованию поверхности разрушения.
Для металлов в формуле появляется gпл – работа по проделыванию пластической деформации:
Формула Ирвина
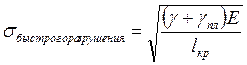
Уравнение Ирвина:
,
где l – длина трещины,
-
коэффициент пропорциональности.
Зная К1С, l можно рассчитать напряжение, при котором трещина начнет быстро расти. Зная величину нагрузки можно определить величину критической трещины.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.