Измерение твердости стальных отливок. Получение значений твердости в зависимости от номера измерения

Министерство образования и науки Российской Федерации

Федеральное государственное автономное образовательное учреждение

Высшего профессионального образования

«Уральский Федеральный Университет им. Первого Президента России Б.Н.Ельцина»

Кафедра «Термообработки и физики металлов»

Отчет по лабораторной работе

По курсу: «Организация и математическое планирование металлофизического эксперимента»

Студент:                                                                                 Кириллова И.Н.

                                                                                                Группа МТ-390702

Преподаватель:                                                                     Водолазский Ф.В

Екатеринбург 2012

Задание:

Измерена твердость стальных отливок.

Полученные значения твердости распределились в зависимости от номера измерения.

Следует определить, подчиняется ли полученная зависимость n_i = f(HB) нормальному закону распределения.

Построить графики, сделать выводы.

Алгоритм:

Дана выборка из генеральной совокупности.

1. Сортируем выборку в порядке возрастания значений, присваиваем каждому номер по порядку.
2. Вычисляем среднее значение, среднеквадратичное отклонение при помощи стандартных статистических функций Microsoft Excel.
3. Проводим разбиение на интервалы:
• Находим количество интервалов по формуле:

и округляем до ближайшего большего целого значения. (При окончательных подсчетах получается количество интервалов, равное m+2, так как границами интервалов не должны являться максимальное и минимальное значения выборки.)

·  Находим ширину интервалов по формуле:

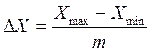
и округляем до первой значащей цифры.

·  Зная количество интервалов и ширину интервалов, производим разбиение.

4. Находим эмпирическую частоту попадания в интервалы значений выборки.
5. Находим накопленную эмпирическую частоту.
6. При помощи стандартной статистической функции Microsoft Excel находим теоретическую частоту попадания значений в интервал, зная границы интервалов, среднее значение выборки и СКО.
7. Находим накопленную теоретическую частоту.
8. Строим графики распределения эмпирических и теоретических частот для сгруппированных данных и диаграмму распределения.
9.  Рассчитываем критерий Пирсона по формуле:

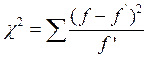
      11.  Сравниваем рассчитанный критерий Пирсона с теоретическим, взятым из таблицы.

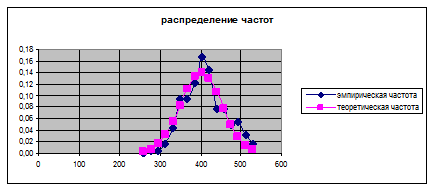
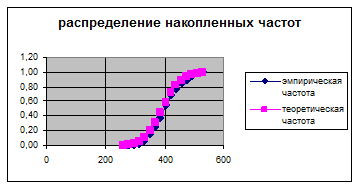
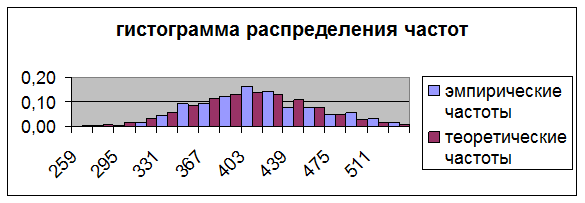
Вывод: , следовательно распределение подчиняется нормальному закону, а расхождения между теоретическими и эмпирическими значениями частот являются случайными.